Table des matières

• 1 Le problème de Helmholtz bidimensionnel.
  • I.1 Présentation de la Formulation ultra-faible.
    • I.1.1 Rappels sur le problème modèle dans le vide.
      • I.1.1.1 Problématique.
      • I.1.1.2 Résultats classiques.
    • I.1.2 Etude de la formulation variationnelle.
      • I.1.2.1 La formulation variationnelle.
      • I.1.2.2 Propriétés de la formulation.
  • I.2 Discrétisation du problème.
    • I.2.1 Approximation de Galerkin.
      • I.2.1.1 Existence et unicité de la solution approchée.
      • I.2.1.2 Remarque sur les notations V et V_h.
      • I.2.1.3 Construction de Galerkin de l'espace V_h.
      • I.2.1.4 Construction des opérateurs discrets.
      • I.2.1.5 Lien avec le problème initial: construction de u_h à partir de x_h.
    • I.2.2 Mise en uvre d'un espace d'approximation particulier.
      • I.2.2.1 Choix de V_h.
      • I.2.2.2 Construction du système linéaire.
    • I.2.3 Solution du système matriciel.
      • I.2.3.1 Inversibilité de D, propriété de M=D^-1C.
      • I.2.3.2 Construction d'un algorithme itératif.
  • I.3 Analyse de la méthode.
    • I.3.1 Notion d'ordre de convergence et rappels sur la méthode des éléments finis.
    • I.3.2 Etude numérique de l'ordre de convergence.
      • I.3.2.1 Calcul numérique de l'erreur.
      • I.3.2.2 Une simulation informatique de calcul d'erreur.
      • I.3.2.3 Calculs d'ordre dans le cas homogène: f=0.
      • I.3.2.4 Calculs d'ordre dans le cas non homogène: $f\ne 0$.
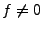      • I.3.2.5 Bilan: lois approchées de convergence numérique.
      • I.3.2.6 Conclusion de l'étude numérique de l'ordre.
    • I.3.3 Etude théorique de l'ordre de convergence.
      • I.3.3.1 Estimation du résidu.
      • I.3.3.2 Une estimation au bord en norme de Sobolev négatif.
      • I.3.3.3 Estimations d'énergie sur la frontière.
      • I.3.3.4 Etude de l'erreur d'interpolation.
      • I.3.3.5 Bilan: majorations de l'ordre de convergence.
    • I.3.4 Conditionnement de la matrice de produit scalaire.
      • I.3.4.1 Majoration théorique du conditionnement.
      • I.3.4.2 Evolution numérique du conditionnement.
      • I.3.4.3 Conclusion sur le problème de l'inversion de la matrice D.
  • I.4 Résultats numériques.
    • I.4.1 Observation des valeurs des champs.
      • I.4.1.1 Cas d'une source d'énergie ponctuelle.
      • I.4.1.2 Deux problèmes de diffraction, Dirichlet et Neumann homogènes.
    • I.4.2 Application à des problèmes de scattering.
      • I.4.2.1 Présentation des tests.
      • I.4.2.2 Notion de Section Efficace Radar.
      • I.4.2.3 Diffraction sur un ballon de football.
      • I.4.2.4 Diffraction sur un profil NACA.
    • I.4.3 Vitesse de convergence de l'algorithme itératif.
  • I.5 Extension au cas des coefficients variables.
    • I.5.1 Présentation du problème et formulation.
      • I.5.1.1 Cadre du problème.
      • I.5.1.2 Nouvelle formulation variationnelle.
      • I.5.1.3 Propriétés de la formulation.
    • I.5.2 Approximation de Galerkin.
      • I.5.2.1 Construction des opérateurs discrétisés.
      • I.5.2.2 Définition et construction de u_h à partir de x_h.
      • I.5.2.3 Choix de l'espace d'approximation et résolution du système linéaire.
    • I.5.3 Conclusion de l'étude du problème à coefficients variables.
  
  
• 2 Le problème de Maxwell tridimensionnel.
  • II.7 Construction de la formulation variationnelle.
    • II.7.1 Rappels sur le problème de Maxwell.
      • II.7.1.1 Problème physique.
      • II.7.1.2 Cadre mathématique usuel et résultats d'existence et d'unicité.
      • II.7.1.3 Découplage des équations de Maxwell.
    • II.7.2 La formulation ultra-faible et ses propriétés.
      • II.7.2.1 Partition du domaine tridimensionnel et notations.
      • II.7.2.2 Relation vérifiée par la solution des équations de Maxwell.
      • II.7.2.3 Réciproque, mise en place de la formulation ultra-faible.
      • II.7.2.4 Définition des opérateurs formels.
      • II.7.2.5 Forme synthétique.
      • II.7.2.6 Propriétés des opérateurs.
  • II.8 Discrétisation du problème de Maxwell.
    • II.8.1 Approximation de type Galerkin.
      • II.8.1.1 Construction de l'espace d'approximation V_h.
      • II.8.1.2 Construction des opérateurs du système linéaire.
      • II.8.1.3 Résolution du système linéaire.
      • II.8.1.4 Construction des traces tangentielles des champs.
    • II.8.2 Un choix particulier de l'espace V_h.
      • II.8.2.1 Construction de solutions du problème dual adjoint.
      • II.8.2.2 Construction d'un espace d'approximation particulier.
      • II.8.2.3 Particularité avantageuse de l'espace d'approximation.
    • II.8.3 Un choix important, le choix d'une base de V_h.
      • II.8.3.1 Choix des polarisations.
      • II.8.3.2 Choix des directions de propagation sur la sphère unité.
  • II.9 Analyse de la méthode sur le problème de Maxwell tridimensionnel.
    • II.9.1 Etude de l'erreur d'interpolation.
      • II.9.1.1 Etude du noyau de la matrice M des coefficients de Taylor des fonctions de base.
      • II.9.1.2 Etude de l'image de la matrice M.
      • II.9.1.3 Bilan de l'étude de l'erreur d'interpolation.
    • II.9.2 Etude de l'ordre de convergence de la méthode.
      • II.9.2.1 Une estimation énergétique d'erreur au bord.
      • II.9.2.2 Estimation énergétique au bord sur les traces tangentielles.
      • II.9.2.3 Estimations de l'ordre de convergence.
    • II.9.3 Etude du conditionnement.
  • II.10 Résultats numériques pour le problème de Maxwell.
    • II.10.1 Tests de validation du code.
      • II.10.1.1 Présentation des tests.
      • II.10.1.2 Propagation libre en milieu homogène.
      • II.10.1.3 Notion de SER.
      • II.10.1.4 Diffraction dans le vide sur un cube.
      • II.10.1.5 Diffraction sur un cône.
    • II.10.2 Utilisation optimale.
      • II.10.2.1 Un cas hors de portée des méthodes classiques.
      • II.10.2.2 Intérêt par rapport à une méthode d'éléments finis.
    • II.10.3 Maillages tétraédriques ou hexaédriques.
      • II.10.3.1 Etude d'un cas limite sur-discrétisé.
      • II.10.3.2 Etude exhaustive sur un cas de propagation dans le vide.
    • II.10.4 Conclusion de l'étude du programme ${\mathcal L}ior$.
  
  
• 3 Annexes
  • III.A Mise en uvre informatique de l'espace V_h choisi pour Helmholtz.
  • III.B Mise en uvre informatique de l'espace V_h choisi pour Maxwell.
    • III.B.1 Construction du système linéaire.
      • III.B.1.1 Introduction, notations.
      • III.B.1.2 Forme des matrices.
      • III.B.1.3 Assemblage des matrices.
      • III.B.1.4 Assemblage du second membre, cas particuliers.
    • III.B.2 Reconstruction des champs électrique et magnétique.
      • III.B.2.1 Reconstruction des champs électrique et magnétique dans l'espace.
      • III.B.2.2 Calcul des traces tangentielles.
      • III.B.2.3 Calcul des traces sur le maillage.
    • III.B.3 Calcul d'erreur pour le code Maxwell tridimensionnel.
  • III.C Performances des codes Helmholtz et Maxwell.
    • III.C.1 Définition de l'indice de performance.
    • III.C.2 Visualisation d'un programme fortran par L^ATEX.
    • III.C.3 Liste des tâches effectuées par les deux programmes, Helmholtz et Maxwell.
    • III.C.4 Code Helmholtz bidimensionnel dans le vide.
    • III.C.5 Code Maxwell tridimensionnel avec ou sans matériau.
  • III.D Calcul des termes intégraux du système linéaire.
    • III.D.1 Formules analytiques des intégrales d'ondes planes.
      • III.D.1.1 Formules d'intégration sur un segment: calcul de I₁.
      • III.D.1.2 Formules d'intégration sur un triangle: calcul de I₂.
      • III.D.1.3 Formules de l'intégrale sur un tétraèdre: calcul de I₃.
    • III.D.2 Algorithmes conditionnels de programmation.
      • III.D.2.1 Programmation de I₁.
      • III.D.2.2 Programmation de I₂.
      • III.D.2.3 Programmation de I₃.
    • III.D.3 Recettes d'implémentation sur machine vectorielle.
      • III.D.3.1 Vectorisation du calcul de I₁.
      • III.D.3.2 Vectorisation du calcul de I₂.
      • III.D.3.3 Vectorisation du calcul de I₃.
  • III.E Déterminant de la matrice D du système linéaire quand h tend vers 0.
    • III.E.1 Problème de Helmholtz bidimensionnel.
    • III.E.2 Problème de Helmholtz tridimensionnel.
    • III.E.3 Problème de Maxwell tridimensionnel.
  
  
• Bibliographie
• Index