




suivant: III.D.2 Algorithmes conditionnels de programmation.
monter: III.D.1 Formules analytiques des intégrales d'ondes planes.
précédent: III.D.1.2 Formules d'intégration sur un triangle: calcul
Table des matières
Index
III.D.1.3 Formules de l'intégrale sur un tétraèdre: calcul de I3.
Nous calculons I3 l'intégrale de (III.D.1) sur le tétraèdre
[x1,x2,x3,x4] de volume V et de barycentre  :
:
|
(III.D.6) |
![\begin{displaymath}
I_3 = \displaystyle \int _{[x_1,x_2,x_3,x_4]}{e^{i{{\mathbf k}}{{\mathbf X}}}} \ d \, {{\mathbf X}}\ .
\end{displaymath}](img1334.gif) |
On pose, pour
 modulo 4
modulo 4
et
On effectue le changement de variable affine
dans (III.D.6), ce qui donne
Après simplification, on a
ou
En posant
 ,
,
 et
et
 ,
pour tout n-1 de 0 à 3 modulo 4, on a
,
pour tout n-1 de 0 à 3 modulo 4, on a
avec
|
(III.D.7) |
 |
Finalement, par symétrie, l'intégrale I3 apparaît comme la fonction de  ,
,  et
et  suivante
suivante
|
(III.D.8) |
 |
fonction que l'on sait continue en
 .
.





suivant: III.D.2 Algorithmes conditionnels de programmation.
monter: III.D.1 Formules analytiques des intégrales d'ondes planes.
précédent: III.D.1.2 Formules d'intégration sur un triangle: calcul
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() :
:
![]() modulo 4
modulo 4
![\begin{displaymath}
I_3 = 6V e^{i{{\mathbf k}}\vec{x}_1} \int_{[0,1]} (1-\theta)...
...e 2i(v_{3}-v_{1})}}{\displaystyle -2i(v_{1}-v_{4})} \,d \theta
\end{displaymath}](img1340.gif)
![\begin{displaymath}
I_3 = 6V Z_1 e^{2i (v_2-v_1 ) } \int_{[0,1]} (1-\theta) \fra...
...e 2i(v_{3}-v_{1})}}{\displaystyle -2i(v_{1}-v_{4})} \,d \theta
\end{displaymath}](img1341.gif)


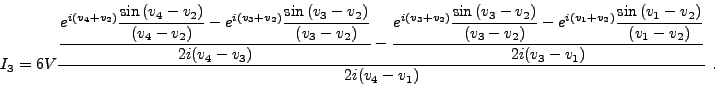
 ,
,
 et
et
 ,
pour tout n-1 de 0 à 3 modulo 4, on a
,
pour tout n-1 de 0 à 3 modulo 4, on a
![]() ,
, ![]() et
et ![]() suivante
suivante