I.2.3.1 Inversibilité de D, propriété de M=D^-1C.

Lemme 5   La matrice D définie par (I.2.18), est hermitienne positive, définie positive si et seulement si les fonctions de base e_kl sont linéairement indépendantes dans $\Omega$. Dans le cas où les fonctions de base e_kl sont des ondes planes à support dans $\Omega _k$ et de direction $\vec{v}_{kl}$, la condition d'indépendance linéaire est assurée si et seulement si les vecteurs d'onde $\vec{v}_{kl}$ sont tous distincts, soit $\forall k, (\forall (i,j), \vec{v}_{ki} \ne \vec{v}_{kj})$.

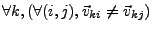On pose alors:

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...cr & b^{'} = D^{-1} b \cr & M = D^{-1} C \ . \crcr}}\, \right.$$ (I.2.23)

Lemme 6   Les valeurs propres de M définie par (I.2.31) sont situées dans le disque complexe de rayon 1, la valeur 1 exclue.

Corollaire 1   Soit $B = (1-\beta)I+\beta M$ (M définie par (I.2.31)) avec $\beta \in ]0;1[$. Les valeurs propres de la matrice B sont situées à l'intérieur du disque complexe unitaire ouvert (la valeur 1 est donc exclue). Notons $\sigma(B)$ le rayon spectral de B. Comme la matrice B est de dimension finie, il existe $\zeta_0 \in ]0;1[$ tel que:

$$% \sigma(B) \leq \zeta_0 \ .$$ (I.2.24)

Soient $\eta$ et $\varepsilon$ des réels strictement positifs avec $\eta \leq 1-\varepsilon < 1$. Alors, pour toute suite réelle $\beta_n \in ]\eta;1-\varepsilon[$ et $B_n=(1-\beta_n)I+\beta_n M$, il existe $\zeta \in ]0;1[$ tel que:

$$\sup_{n \in {\mathbb{N}}} \sigma(B_n) \leq \zeta \ .$$ (I.2.25)

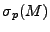On note (figure I.2.3) $\lambda(M)$ une valeur propre de M et $\lambda(B)$ une valeur propre de B. Le cercle de rayon 1 centré sur l'origine délimite le spectre ponctuel $\sigma_p(M)$ de M (ensemble des valeurs propres en dimension finie). L'ensemble hachuré, noté $\sigma_p(B)$ contient les valeurs propres de B. L'introduction du correcteur $\beta \in ]0;1[$ tend globalement à rapprocher de l'origine les valeurs propres de M et permet donc d'améliorer la convergence sur le plan numérique.

Figure I.2.3: Valeurs propres de M et B pour $\beta = 0,6$.