




suivant: I.3.2.6 Conclusion de l'étude numérique de l'ordre.
monter: I.3.2 Etude numérique de l'ordre de convergence.
précédent: I.3.2.4 Calculs d'ordre dans le cas non
Table des matières
Index
D'après les figures (I.3.4), (I.3.5), (I.3.6) et
(I.3.7), il semble que nous pouvons dégager des lois d'ordre de convergence. Nous séparons ces lois en deux cas,
le cas f=0 et le cas 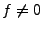 . Pour chacune des normes étudiées, on aura donc deux lois, une pour le problème homogène et une autre pour
le problème non homogène.
. Pour chacune des normes étudiées, on aura donc deux lois, une pour le problème homogène et une autre pour
le problème non homogène.
- Les normes
 et
et
 suivent les lois du
tableau I.3.5.
suivent les lois du
tableau I.3.5.
- La norme
 suit la loi du tableau I.3.5 lorsque
la méthode de calcul utilise la formule d'approximation générale (I.2.23).
suit la loi du tableau I.3.5 lorsque
la méthode de calcul utilise la formule d'approximation générale (I.2.23).
- Les normes
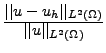 et
et
 suivent
les lois du tableau I.3.6, à l'aide de la formule d'approximation (I.2.27)
qui ne devrait être utilisée que dans le cas homogène.
suivent
les lois du tableau I.3.6, à l'aide de la formule d'approximation (I.2.27)
qui ne devrait être utilisée que dans le cas homogène.
Tableau I.3.5:
Bilan: ordres de convergence en fonction de p
| p nb. de f.b. par élt |
3 4 |
5 6 |
7 8 |
9 10 |
11 12 |
13 14 |
| cas |
Non homogène |
| |
Homogène |
|
|
|
|
|
|
|
Tableau I.3.6:
Bilan: ordres de convergence en fonction de p
| p nb. de f.b. par élt |
3 4 |
5 6 |
7 8 |
9 10 |
11 12 |
13 14 |
| cas |
Non homogène |
| |
Homogène |
|
|
|
|
|
|
|
Remarque 18
On observe une croissance linéaire de l'ordre de convergence en fonction du nombre de fonctions de base p par élément.
En première approximation, la pente de la loi de convergence du problème non homogène est deux fois plus faible que celle du problème homogène.
Remarque 19
Nous avons des résultats numériques plus complets dans l'étude du problème non homogène que dans celle du problème homogène
(d'où les points d'interrogation dans les tableaux
I.3.5 et
I.3.6). En effet, alors que
le conditionnement ne dépend pas du second membre
f du problème (
I.0.1), l'ordre de convergence du
problème non homogène augmente à un taux plus faible que celui du problème homogène, d'environ la moitié. La perte de précision
numérique due au conditionnement importe plus dans un calcul très précis (ce qui est le cas du problème homogène) que dans un calcul moins
précis ((ce qui est le cas du problème non homogène). Ces constatations sont expliquées théoriquement sections
I.3.3.5
et
I.3.4 avec les corollaires
4 et
5 et le
théorème
8.
Remarque 20 Il peut être utile de relire la remarque
18 pour comprendre les différences entre le cas non homogène du
tableau
I.3.5 et du tableau
I.3.6. Ces deux tableaux donnent l'ordre de convergence de
la trace de
u sur

. Dans le cas homogène, on obtient une amélioration d'environ 1/2 de la norme de
u sur

par les formules
(
I.2.27) à la place de l'approximation (
I.2.23).





suivant: I.3.2.6 Conclusion de l'étude numérique de l'ordre.
monter: I.3.2 Etude numérique de l'ordre de convergence.
précédent: I.3.2.4 Calculs d'ordre dans le cas non
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() . Pour chacune des normes étudiées, on aura donc deux lois, une pour le problème homogène et une autre pour
le problème non homogène.
. Pour chacune des normes étudiées, on aura donc deux lois, une pour le problème homogène et une autre pour
le problème non homogène.
 et
et
 suivent les lois du
tableau I.3.5.
suivent les lois du
tableau I.3.5.
 suit la loi du tableau I.3.5 lorsque
la méthode de calcul utilise la formule d'approximation générale (I.2.23).
suit la loi du tableau I.3.5 lorsque
la méthode de calcul utilise la formule d'approximation générale (I.2.23).
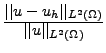 et
et
 suivent
les lois du tableau I.3.6, à l'aide de la formule d'approximation (I.2.27)
qui ne devrait être utilisée que dans le cas homogène.
suivent
les lois du tableau I.3.6, à l'aide de la formule d'approximation (I.2.27)
qui ne devrait être utilisée que dans le cas homogène.