I.5.2.2 Définition et construction de u_h à partir de x_h.

Nous décrivons comment définir et calculer une approximation de u (la solution du problème de Helmholtz), notée u_h à partir de x_h solution de (I.5.36). Il y a deux techniques indépendantes d'approximation de u:

i) Reconstruction de u_h sur $\partial \Omega_k$.

Comme dans le cas sans coefficient, on montre aisément que la trace de u sur V est liée à x par

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...I+\Pi)x+g] & \mbox{ sur } \Gamma_{k} \ , \cr \crcr}}\, \right.$$ (I.5.20)

et l'on définit u_h sur les arêtes du maillage par

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...I+\Pi)x_h+g] & \mbox{ sur } \Gamma_k \ . \cr \crcr}}\, \right.$$ (I.5.21)

Pratiquement, l'équation (I.5.41) signifie que:

1. nous construisons u_h sur $\Gamma$ par
   

   $$2i\omega \sigma(u_h)_{\vert\Gamma_k} = g+(1+{{\mathit Q}}_k)... ...hop{{\mathbf {\nabla }}}\nolimits +i\omega \sigma )e_{kl}} \ ,$$ (I.5.22)

   
   

2. et nous construisons u_h sur $\Sigma_{kj}$ par
   

   $$2i\omega \sigma(u_h)_{\vert\Sigma_{kj}} = \sum_{l(k)}{x_{kl}... ...hop{{\mathbf {\nabla }}}\nolimits +i\omega \sigma )e_{jl}} \ .$$ (I.5.23)

   
   

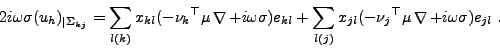ii) Reconstruction de u_h dans $\Omega$.

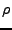Comme pour le problème de Helmholtz sans coefficient, lorsque f=0 et $\mu$ et $\rho$ réels, nous pouvons reconstruire u_h par

$$\null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil$... ...\Omega_k} = \sum_{l=1}^{p}{x_{kl} \, e_{kl}} \ . \cr \crcr}}\,$$ (I.5.24)

En effet, dans ce cas, l'opérateur de relèvement, E, est linéaire.