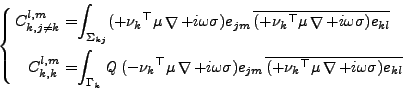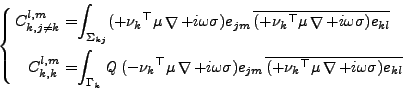suivant: I.5.2.2 Définition et construction de uh à
monter: I.5.2 Approximation de Galerkin.
précédent: I.5.2 Approximation de Galerkin.
Table des matières
Index
- i)
- Les coefficients de la matrice D définis par
Dk,j l,m = (zjm,zkl)V sont donnés par
|
(I.5.17) |
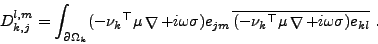 |
On a donc
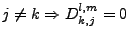 .
.
- ii)
- Les coefficients de la matrice C définis par
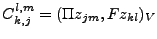 sont:
sont:
|
(I.5.18) |
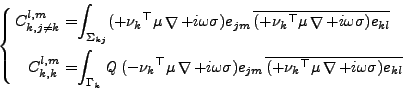 |
- iii)
- Le second membre b est construit par
bk,l = (b,zkl)V:
|
(I.5.19) |
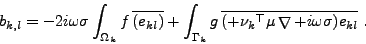 |
Cessenat Olivier
2007-04-21