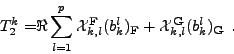suivant: III.C Performances des codes Helmholtz et Maxwell.
monter: III.B Mise en uvre informatique de l'espace
précédent: III.B.2.3.2 Un calcul possible des champs électrique
Table des matières
Index
III.B.3 Calcul d'erreur pour le code Maxwell tridimensionnel.
Le but de cette section est de montrer que le calcul d'erreur dans le cas où la solution exacte est une onde plane présente la même difficulté qu'un assemblage de matrice.
Nous présentons ici le calcul de la norme d'erreur de bord
dans le cas où la quantité exacte
 est connue sous la forme
est connue sous la forme
La quantité approchée est calculée par
On calcule donc la norme de l'erreur par
On pose
Calcul de T1k. Dans le vide, on calcule que
Calcul de T2k. On remarque que ce terme est calculé de la même façon que le second membre du couplage des fonctions de base avec la fonction de bord g. On note abusivement,
(puisque
 n'est pas égal à g, la condition sur le bord extérieur d'un calcul de diffraction en champ total)
n'est pas égal à g, la condition sur le bord extérieur d'un calcul de diffraction en champ total)
et l'on a





suivant: III.C Performances des codes Helmholtz et Maxwell.
monter: III.B Mise en uvre informatique de l'espace
précédent: III.B.2.3.2 Un calcul possible des champs électrique
Table des matières
Index
Cessenat Olivier
2007-04-21
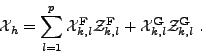
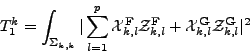
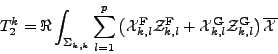
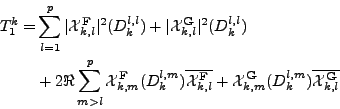
![]() n'est pas égal à g, la condition sur le bord extérieur d'un calcul de diffraction en champ total)
n'est pas égal à g, la condition sur le bord extérieur d'un calcul de diffraction en champ total)