suivant: III.D.3 Recettes d'implémentation sur machine vectorielle.
monter: III.D.2 Algorithmes conditionnels de programmation.
précédent: III.D.2.2 Programmation de I2.
Table des matières
Index
III.D.2.3 Programmation de I3.
Rappelons que I3 (III.D.8) est donné par
|
(III.D.16) |
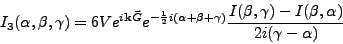 |
en définissant les fonctions I et f par
|
(III.D.17) |
 |
ou en définissant
Zn = ei<I>k<I>Xn où
<I>Xn est la position du n-ième sommet du tétraèdre,
La programmation de cette intégrale volumique est très compliquée. Nous donnons l'algorithme de calcul sans explication, cet algorithme étant dans la ligne logique des algorithmes présentés
dans les sections III.D.2.1 et III.D.2.2.
Nous laissons au lecteur le soin de calculer  et
et 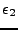 de façon à maximiser la précision des calculs quels que soient les paramètres de la fonction I3.
de façon à maximiser la précision des calculs quels que soient les paramètres de la fonction I3.
- Pour
 :
:
- Pour
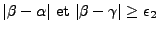 :
:
- Pour
 , on calcule alors I3 en remplaçant
, on calcule alors I3 en remplaçant  par 1.
par 1.
- Pour
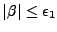 , on calcule alors I3 en remplaçant
, on calcule alors I3 en remplaçant 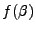 par 1.
par 1.
- Pour
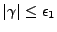 , on calcule alors I3 en remplaçant
, on calcule alors I3 en remplaçant 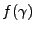 par 1.
par 1.
- Pour
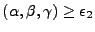 , on calcule I3 simplement par la formule III.D.16.
, on calcule I3 simplement par la formule III.D.16.
- Pour
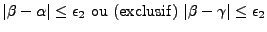 , comme le problème est symétrique, on suppose:
, comme le problème est symétrique, on suppose:
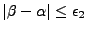 .
On doit donc remplacer
.
On doit donc remplacer
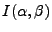 par un développement:
par un développement:
- Pour
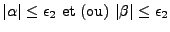 , on calcule alors
, on calcule alors
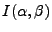 par son développement limité:
par son développement limité:
|
(III.D.18) |
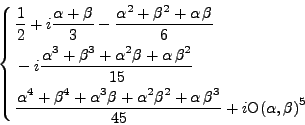 |
- Pour
 , on calcule alors
, on calcule alors
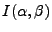 par:
par:
|
(III.D.19) |
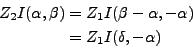 |
où le dénominateur de
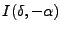 est forcément assez grand.
On remplace
est forcément assez grand.
On remplace  par:
par:
- Pour
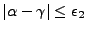 :
:
- Pour
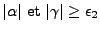 , on a
, on a
avec
 .
On se ramène alors à l'étude précédente avec
.
On se ramène alors à l'étude précédente avec
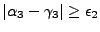 .
.
- Pour
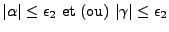 :
:
- Pour
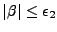 , on effectue un développement limité complet de I3:
, on effectue un développement limité complet de I3:
|
(III.D.20) |
 |
- Pour
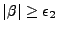 , on a
, on a
avec
 .
On se ramène alors à l'étude précédente avec
.
On se ramène alors à l'étude précédente avec
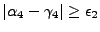 .
.





suivant: III.D.3 Recettes d'implémentation sur machine vectorielle.
monter: III.D.2 Algorithmes conditionnels de programmation.
précédent: III.D.2.2 Programmation de I2.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() et
et ![]() de façon à maximiser la précision des calculs quels que soient les paramètres de la fonction I3.
de façon à maximiser la précision des calculs quels que soient les paramètres de la fonction I3.