II.7.2.1 Partition du domaine tridimensionnel et notations.

Comme pour le problème de Helmholtz bidimensionnel, nous réalisons une partition du domaine tridimensionnel $\Omega$.

Notation 2 (Rappels et notations des faces de bord $\Sigma _{kk}$)   Soit $\Omega$ un domaine borné de ${\mathbb{R}}^3$ partitionné en K domaines $\Omega _k$ lipschitziens. Pour un élément $\Omega _k$ donné, nous considérons un de ses voisins $\Omega_j$. L'interface entre $\Omega _k$ et $\Omega_j$ est notée $\Sigma_{kj}$ comme pour Helmholtz. Considérons un élément $\Omega _k$ qui possède une frontière libre, c'est-à-dire sur laquelle il n'y a pas de voisin $\Omega_j$. Nous avons noté $\Gamma_k$ une telle frontière dans l'étude du problème de Helmholtz. Dans l'étude du problème de Maxwell avec matériaux, nous verrons qu'une telle notation n'est pas très judicieuse. En effet, d'une part elle risque d'introduire une confusion avec les notations classiques définissant $\Gamma_k$ comme étant le bord de la maille $\Omega _k$, d'autre part cette notation crée une asymétrie entre les types de frontières alors qu'elles jouent le même rôle lorsque l'on s'intéresse simplement au bord de $\Omega _k$. C'est pourquoi nous appellerons dorénavant une telle frontière $\Sigma _{kk}$, ce qui permet d'écrire que

$$% \partial \Omega_k = \bigcup_{j(k), \ \Omega_j \mbox{ voisin... ...mbox{ ou } j=k \mbox{ sur une face fronti{\\lq e}re}} \Sigma_{kj}$$ (II.7.45)

où j(k) décrit l'ensemble des voisins de $\Omega _k$ qui sont des éléments de la partition de $\Omega$, plus la frontière libre éventuelle $\Sigma _{kk}$. Par la suite, lorsqu'il n'y aura pas de risque de confusion, j(k) sera noté j. La figure II.7.2 résume ces notations: il s'agit d'un exemple de partition de domaine sous la forme d'un maillage en éléments hexaédriques dont on effectue une coupe dans le plan de la feuille.

Figure II.7.2: Illustration de la définition de $\Sigma _{kk}$.

Pour un élément $\Omega _k$ quelconque nous notons:

• $\nu_k$ une normale à l'élément $\Omega _k$,
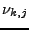• $\nu_{k,j}$ une normale à l'interface $\Sigma_{k,j}$.

Définissons maintenant les fonctions 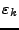$\varepsilon _{k}$, $\varepsilon _{kk}$ et $\varepsilon _{kj}$ introduites dans la formulation variationnelle à partir de la perméabilité $\varepsilon$. Nous définirons de la même façon les fonctions $\mu_{k}$, $\mu_{kk}$ et $\mu_{kj}$.

1. La fonction 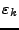$\varepsilon _{k}$ est la restriction de $\varepsilon$ à l'élément $\Omega _k$,
   

   $$% \varepsilon _{k}= \varepsilon _{\vert\Omega_k} \ .$$ (II.7.46)

   
   

2. La fonction réelle $\varepsilon _{kj}$ est la valeur absolue de la moyenne géométrique à l'interface $\Sigma_{kj}$ de la fonction $\varepsilon$ sur $\Omega _k$ et sur $\Omega_j$,
   

   $$\varepsilon _{kj}= \vert \sqrt{\varepsilon _{k}\varepsilon _{j}} \vert \ .$$ (II.7.47)

   
   

3. Sur une face frontière $\Sigma _{kk}$, la fonction réelle $\varepsilon _{kk}$ vaut d'après (II.7.60):
   

   $$% \varepsilon _{kk}= \vert \varepsilon _{k}\vert \ .$$ (II.7.48)

   
   
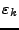   Ne pas confondre $\varepsilon _{kk}$ et $\varepsilon _{k}$, ces fonctions sont égales sur $\Sigma _{kk}$ si et seulement si 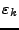$\varepsilon _{k}$ est réelle (positive par hypothèse sur $\varepsilon$, cf (II.7.1)).

Remarque 33   Notons l'intérêt du choix de la moyenne géométrique plutôt que de la moyenne arithmétique pour la définition des fonctions approchées $\varepsilon _{kk}$ et $\mu_{kk}$ dans le cas d'une discontinuité des permittivité et perméabilité entre $\Omega _k$ et $\Omega_j$:

$$% \left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\st... ...r}}\, \right. \Longrightarrow \varepsilon _{kj}\mu_{kj}= 1 \ .$$ (II.7.49)

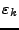
D'autre part, si $\varepsilon _{k}$ est réelle, alors

$$\frac{\displaystyle \varepsilon _{kj}}{\displaystyle \sqrt{\varepsilon _{k}}} = \vert\sqrt{\varepsilon _{j}}\vert$$ (II.7.50)

ne dépend plus de k. Enfin, les fonctions réelles $\varepsilon _{kj}$ et $\mu_{kj}$ vérifient

$$\left\vert \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\... ...\varepsilon _{jk}\cr & \mu_{kj}= \mu_{jk}\cr \crcr}}\, \right.$$ (II.7.51)

Comme pour le problème de Helmholtz, définissons l'espace fonctionnel V de la formulation ultra-faible. Notons toujours que cet espace dépend du maillage, mais que ce n'est pas un espace de discrétisation de dimension finie.

Définition 6   L'espace de travail V est l'espace de Hilbert produit des espaces de Hilbert L²_t() définis en II.7.23:

$$%\label{equation.m3dnotations.019} V = \prod_{k=1}^{K}{L^2_t(\partial \Omega_k)} \ ,$$ (II.7.52)

ou, de façon équivalente, par,

$$V = \prod_{k=1}^{K}{ \prod_{j(k)}{ L^2_t(\Sigma_{kj}) }} \ .$$

L'espace de travail est muni du produit scalaire naturel

$$% \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil... ...line{{{\mathcal{Y}}}_{\vert\partial \Omega_k}}}} \cr \crcr}}\,$$ (II.7.53)

qui définit la norme ||.||_V et la norme induite d'un opérateur $A \in V$ par:

$$% \vert\vert A\vert\vert = \sup_{x \ne 0}\frac{\displaystyle ... ... Ax\vert\vert _V}{\displaystyle \vert\vert x\vert\vert _V} \ .$$ (II.7.54)