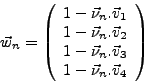suivant: III.E.2 Problème de Helmholtz tridimensionnel.
monter: III.E Déterminant de la matrice D du
précédent: III.E Déterminant de la matrice D du
Table des matières
Index
III.E.1 Problème de Helmholtz bidimensionnel.
Pour le triangle numéroté par l'indice k, on définit les quantités suivantes:
- les trois longueurs notées L1,L2,L3,
- les trois normales notées
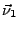 ,
, 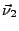 et
et 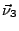 ,
,
- le périmètre noté P,
- la surface notée S.
On s'intéresse au cas asymptotique
 et p=3 pour un problème bidimensionnel.
et p=3 pour un problème bidimensionnel.
Théorème 19
On introduit la matrice limite Dr définie par
|
(III.E.1) |
 |
ainsi que les quantités réduites indexées
(Pr,Sr,L1r,L2r,L3r) qui sont obtenues des précédentes en divisant par 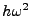 sauf Sr où l'on divise par
sauf Sr où l'on divise par  .
Alors:
.
Alors:
- La matrice limite Dr existe et est inversible.
- Le déterminant de Dr se calcule par le produit de deux quantités, l'une faisant intervenir la géométrie du triangle, l'autre la répartition des fonctions de base. Des ondes
planes équiréparties maximisent le déterminant de Dr et il vaut alors
|
(III.E.2) |
 |
- La majoration du conditionnement à partir du déterminant est maximale pour des ondes planes équiréparties et on majore le conditionnement de D par
|
(III.E.3) |
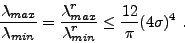 |
dont le terme majorant  (I.2.4) est minimal dans le cas d'un triangle équilatéral.
(I.2.4) est minimal dans le cas d'un triangle équilatéral.
La preuve de ce théorème fait l'objet de toute cette section. La preuve est longue, technique et calculatoire. Elle est effectuée en plusieurs étapes et suit l'ordre de présentation des
résultats effectuée théorème 19:
- a)
- simplification du déterminant de la matrice D (où l'on ne garde que les termes d'ordre 1 en h) en un produit dépendant de l'unité d'échelle du triangle h et un terme
indépendant de h,
- b)
- découplage du déterminant (toujours de la matrice D où l'on n'a gardé que les termes du premier ordre en h) entre les termes géométriques et les fonctions de base,
- c)
- optimisation du déterminant en fonction du choix des directions de propagation des ondes planes,
- d)
- récapitulatif des points précédents et fin du calcul du déterminant (ceci montre le point 2 du théorème 19),
- e)
- majoration du conditionnement (point 3 du théorème 19).
Le lemme suivant donne la forme de la matrice réduite Dr.
Lemme 29
Les termes de la matrice Dk (calculés chapitre III.A) sont équivalents au premier
ordre à la matrice, encore notée D (par abus) dans toute cette section, dont les termes Dl,m pour
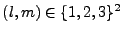 sontIII.E1
sontIII.E1
|
(III.E.4) |
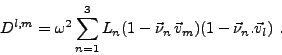 |
Les termes de la matrice réduite sont donc
|
(III.E.5) |
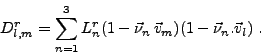 |

On pose:
|
(III.E.6) |
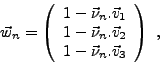 |
et D sera la matrice définie par
|
(III.E.7) |
![\begin{displaymath}%
\null\,\vcenter{\openup1\jot \let\\ =\@
\ialign{\strut\hfi...
...+L_3D_3) \cr
& D_n = [\vec{w}_n\otimes\vec{w}_n] \ .
\crcr}}\,
\end{displaymath}](img1502.gif) |
Remarque 54 En toute rigueur, on a
On pose en outre, dans toute cette section,
|
(III.E.8) |
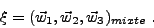 |
a) Simplification du déterminant de D.
Lemme 30
La matrice D est inversible si et seulement si les trois vecteurs 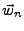 sont indépendants dans
sont indépendants dans
 :
:
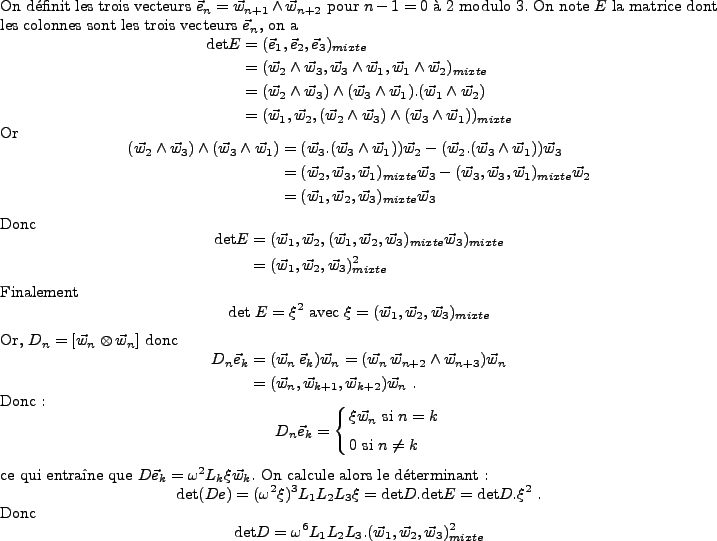
b) Découplage du déterminant entre les termes géométriques et les fonctions de base.

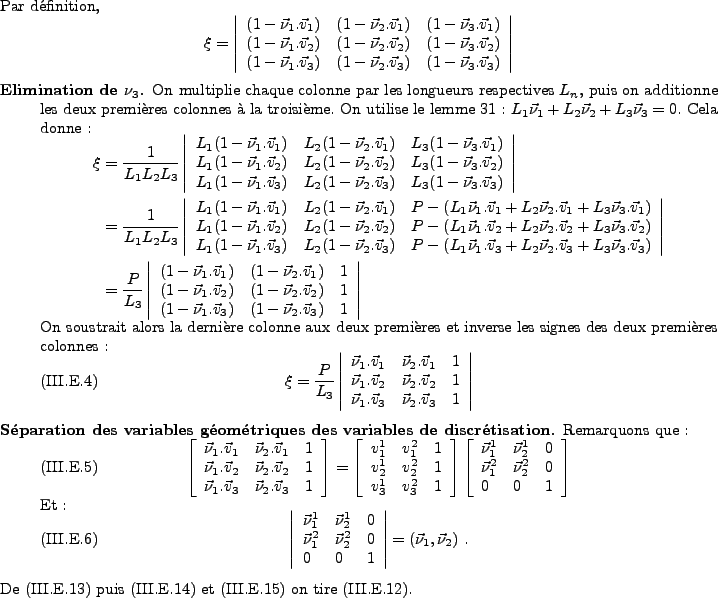
c) Optimisation du déterminant.
Le calcul du produit mixte de trois vecteurs donne le volume du simplexe
déterminé par ces trois vecteurs: nous avons pensé
que le déterminant est de module maximal
pour des vecteurs vn équirépartis dans le plan. C'est ce que nous allons montrer dans le lemme suivant.
Lemme 33
On montre que 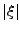 est maximal pour des vecteurs vn équirépartis dans le plan.
est maximal pour des vecteurs vn équirépartis dans le plan.
![\begin{proof}
On pose, pour $(\alpha,\beta) \in ]-\pi,\pi]^2$\ et $\alpha \ne \b...
... = \frac{\displaystyle 3\sqrt{3}}{\displaystyle 2} \ .
\end{equation}\end{proof}](img1514.gif)
d) Récapitulatif et fin du calcul du déterminant.
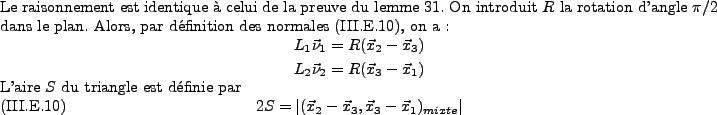

e) Majoration du conditionnement.
Nous allons montrer le dernier point du théorème 19.

f) Remarques.
Remarque 55
Ce résultat est généralisable au problème de Helmholtz scalaire dans un espace tridimensionnel avec un tétraèdre
et 4 fonctions de base (cf Annexe
III.E.2).
En revanche, on ne peut pas le généraliser au cas des
n-polygones avec
n fonctions de base
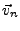
.
On peut en donner un contre-exemple pour
n=4. Prenons
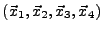
un carré,
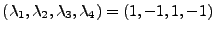
.
Les vecteurs
wn sont alors liés.
Remarque 56
Il est trivial de remarquer que la matrice limite
Dr (

)
avec quatre fonctions de base ou plus (

) n'est pas inversible.
En effet, la nouvelle matrice
Dr obtenue s'écrira toujours sous la forme (en gardant toujours le même sens à la notation en indice
r):
avec
Le rang de la matrice
Dr est au plus de trois, pour une matrice de taille
p x
p et

.





suivant: III.E.2 Problème de Helmholtz tridimensionnel.
monter: III.E Déterminant de la matrice D du
précédent: III.E Déterminant de la matrice D du
Table des matières
Index
Cessenat Olivier
2007-04-21
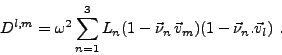
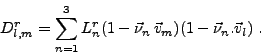

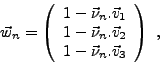
![\begin{displaymath}%
\null\,\vcenter{\openup1\jot \let\\ =\@
\ialign{\strut\hfi...
...+L_3D_3) \cr
& D_n = [\vec{w}_n\otimes\vec{w}_n] \ .
\crcr}}\,
\end{displaymath}](img1502.gif)
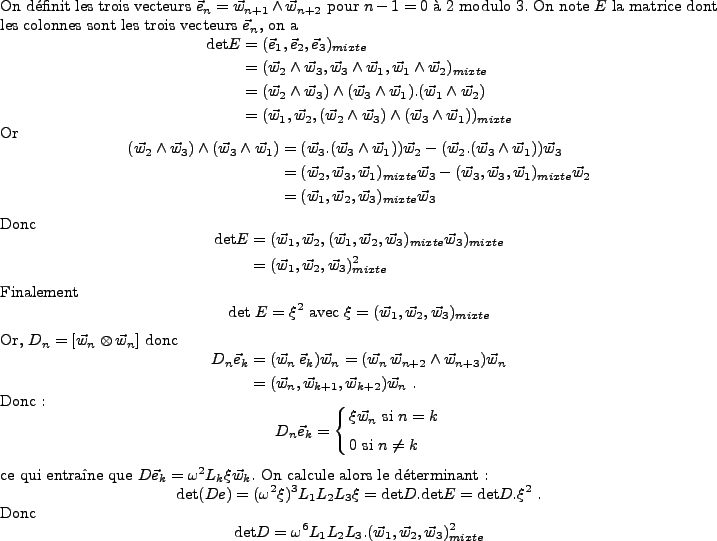
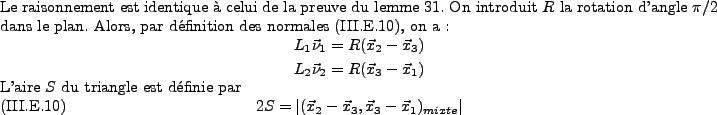

![\begin{displaymath}
\null\,\vcenter{\openup1\jot \let\\ =\@
\ialign{\strut\hfil...
..._3^rD_3) \cr
& D_n = [\vec{w}_n\otimes\vec{w}_n] \ ,
\crcr}}\,
\end{displaymath}](img1523.gif)