I.2.1.4 Construction des opérateurs discrets.

Nous construisons les termes correspondant à la formulation (I.1.27). La formulation discrétisée (I.2.1) de (I.1.25) conduit au système (I.2.17), forme discrète de (I.1.27).

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...X \in {\mathbb{C}}^{pK} \cr & (D-C)X = b \cr \crcr}}\, \right.$$ (I.2.10)

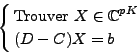La matrice notée D est la matrice du produit scalaire dans V_h. La matrice notée C est la matrice de la forme bilinéaire $(\Pi x_h,Fy_h)$. Le second membre, par abus de langage, est toujours noté b.

i)

Les coefficients de la matrice D définis par D_k,j ^l,m = (z_jm,z_kl)_V sont:

$$D_{k,j} ^{l,m} = \int_{ \partial \Omega_k} ( -\partial_{\nu_... ..._{jm} \, \overline{ ( -\partial_{\nu_k} +i\omega )e_{kl} } \ .$$ (I.2.11)

Remarque 4   Pour $j \ne k$ les supports de e_jm et e_kl sont disjoints, donc D_k,j ^l,m=0.

ii)

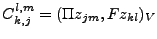Les coefficients de la matrice C sont, soit une intégrale sur les interfaces $\Sigma_{kj}$ et définis par $C_{k,j} ^{l,m} =(\Pi z_{jm},Fz_{kl})_V$, soit une intégrale sur une face de bord $\Gamma_k$ et définis par $C_{k} ^{l,m}=(\Pi z_{km},Fz_{kl})_V$.

$$C_{k,j} ^{l,m} = \int_{\Sigma_{kj}} (+\partial_{\nu_k} +i\omega )e_{jm} \, \overline{(+\partial_{\nu_k} + i \omega )e_{kl} }$$ (I.2.12)

$$C_{k} ^{l,m} = \int_{\Gamma_k} {{\mathit Q}}_k \, (-\partial... ...a )e_{jm} \, \overline{(+\partial_{\nu_k} + i \omega)e_{kl} }$$ (I.2.13)

iii)

Le second membre b est défini par b_k,l = (b,z_kl)_V (le second membre de la formulation discrète et le second membre du problème variationnel sont abusivement notés de la même façon) soit

$$\null\,\vcenter{\openup1\jot \let\\ =\@ \ialign{\strut\hfil... ... \overline{(+\partial_{\nu_k} +i\omega )e_{kl} } \ . \crcr}}\,$$ (I.2.14)

Nous considérons la figure I.2.1 de maillage d'un rectangle en triangles. Nous présentons la forme (essentiellement creuse) des matrices D et C.

Figure I.2.1: Un exemple de maillage d'un rectangle en triangles.

i)

La matrice D est diagonale par blocs: D_kj=0 pour $k \ne j$:

$$D = \begin{array}{\vert ccccc\vert} D_1 & 0 & \ldots & & \\ ... ...\\ \end{array} \mbox{ o{\\lq u} $ (D_k)_{(l,m)}=D_{kk}^{lm} $ .}$$

ii)

La matrice C est non nulle sur des blocs diagonaux correspondant aux éléments $\Omega _k$ ayant une face sur le bord extérieur $\Gamma_k$ (le terme C_k,k est nul si $\Gamma_k = \emptyset$):

$$\mbox{Diag }(C) = \left[ \begin{array}{cccccc} C_{1,1} & 0 &... ...ots & \vdots & \vdots & \vdots & 0 \\ \end{array}\right] \ .$$

iii)

Le terme non diagonal de couplage de C est nul au bord. Nous donnons la forme générale de ce terme, et les blocs précis pour les couplages des 5 premiers éléments du maillage:

$$\left[ \begin{array}{ccc} \begin{array}{cccccccc} 0 & C_{1,2... ...s & \vdots & \vdots & \ldots \\ \end{array}\end{array}\right]$$

où (j₁,j₂,j₃) sont les indices des trois voisins d'un élément $\Omega_{k}$ de la triangulation.