




suivant: I.4.2.3 Diffraction sur un ballon de football.
monter: I.4.2 Application à des problèmes de scattering.
précédent: I.4.2.1 Présentation des tests.
Table des matières
Index
Le lecteur peut se reporter à [55] pour une définition de la SER. Le calcul de la SER est pour nous un moyen de comparer notre code à un code existant et fiable,
un code d'équations intégrales (IE) appelé SHF2D et développé au CEA-CEL-V par P. Bonnemason, B. Stupfel [8]. Ce code simule des Conditions aux Limites de
Neumann et de Dirichlet à l'aide d'un matériau parfaitement isolant ou conducteur, c'est-à-dire d'impédance nulle ou infinie.
Nous utilisons la formule (I.3.27 p. ![[*]](crossref.gif) ) dans laquelle
) dans laquelle
 étant l'angle bistatique d'observation
de l'onde incidente
étant l'angle bistatique d'observation
de l'onde incidente 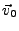 :
:
|
(I.4.3) |
 |
En utilisant la relation vérifiée par g (I.3.6), la définition (I.2.16) de xh, et la condition aux
limites (I.2.24) définissant uh à l'aide de xh, nous avons:
Nous calculons le terme intégral de l'équation (I.4.3) sur  :
:
|
(I.4.4) |
 |
Ceci remplacé dans l'équation (I.4.3) permet un calcul exact de l'amplitude de diffusion.
Selon la polarisation, nous multiplions  de l'équation (I.4.3) par -1 dans le mode de polarisation TM (qui correspond à prendre des
conditions aux limites de Dirichlet sur
de l'équation (I.4.3) par -1 dans le mode de polarisation TM (qui correspond à prendre des
conditions aux limites de Dirichlet sur  ), et par i dans le mode de polarisation TE (qui correspond à prendre des conditions aux limites de Neumann sur
), et par i dans le mode de polarisation TE (qui correspond à prendre des conditions aux limites de Neumann sur  ).
Par définition, la SER est
).
Par définition, la SER est
 . Notons qu'en bidimensionnel cette quantité est en toute rigueur appelée LER et se mesure en dB.m.
. Notons qu'en bidimensionnel cette quantité est en toute rigueur appelée LER et se mesure en dB.m.





suivant: I.4.2.3 Diffraction sur un ballon de football.
monter: I.4.2 Application à des problèmes de scattering.
précédent: I.4.2.1 Présentation des tests.
Table des matières
Index
Cessenat Olivier
2007-04-21
![[*]](crossref.gif) ) dans laquelle
) dans laquelle
![[*]](crossref.gif) ) dans laquelle
) dans laquelle
![]() étant l'angle bistatique d'observation
de l'onde incidente
étant l'angle bistatique d'observation
de l'onde incidente ![]() :
:

