Remarque 28 Dans la démonstration du théorème
7, le fait que
u est solution d'un problème homogène est essentiel.
Cependant, dans le cas
n=1, le résultat est encore vrai pour
u solution d'un problème de Helmholtz non homogène. En effet, on a
p=2
n+1=3=(
n+2)(
n+1)/2 fonctions de base.
L'espace vectoriel
K (
I.3.54) est de dimension 3 car
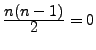
.
Pour tout
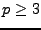
,
x défini par (
I.0.3) et
u la solution du problème de
Helmholtz homogène ou non homogène (
I.0.1), on a:
|
(I.3.19) |
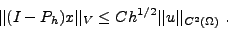 |
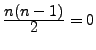 .
Pour tout
.
Pour tout 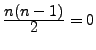 .
Pour tout
.
Pour tout ![\begin{displaymath}%
\forall s > [(p-1)/2]-1/2 \left\{ \null\,\vcenter{\openup\j...
... \vert\vert u\vert\vert _{C^{2}(\Omega)} \cr
\crcr}}\,
\right.
\end{displaymath}](img331.gif)
