I.3.3.2 Une estimation au bord en norme de Sobolev négatif.

Nous réalisons cette estimation par une technique de dualité. C'est l'équivalent du lemme d'Aubin-Nitsche. Le résultat présenté sera utile dans l'étude du cas $f\ne 0$.

Théorème 6   Soit $\Omega$ un domaine borné de ${\mathbb{R}}^2$ de frontière $\Gamma$ assez régulière, nous prendrons $C^{\infty}$ pour simplifier. Supposons ${{\mathit Q}}$ (l'opérateur de bord du problème de Helmholtz (I.0.1)) une fonction à valeur complexe et $\vert{{\mathit Q}}\vert \leq 1$. Considérons $x \in V$ la solution de (I.1.27) et $x_h \in V_h$ la solution de (I.2.1). Soit P_h le projecteur orthogonal sur l'espace V_h. Soit s > 1/2 et $\psi \in H^{s}(\Gamma)$. Nous définissons w par:

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...\omega)w+ \psi & \mbox{ sur } \Gamma \ . \cr \crcr}}\, \right.$$ (I.3.11)

et $y(\psi) \in V$ par

$$\null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil$... ...u_k}+i \omega)w & \mbox{ sur } \partial \Omega_k \ . \crcr}}\,$$

Alors, on a $\forall s > 1/2$

$$\mbox{ \fbox{$ \vert\vert x-x_h\vert\vert _{H^{-s}(\Gamma)} ... ...\displaystyle \vert\vert\psi\vert\vert _{H^{s}(\Gamma)}}}} $}}$$ (I.3.12)

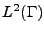
Remarque 21   L'intérêt de (I.3.22) vient de ce que $$\sup_{\psi \in H^{s}(\Gamma)} \frac{\displaystyle \vert\vert(I-P_h)y(\psi)\vert\vert}{\displaystyle \vert\vert\psi\vert\vert _{H^{s}(\Gamma)}}$$ tend vers zéro avec h comme l'indique le théorème (7). L'estimation obtenue est meilleure dans un espace de Sobolev négatif $H^{-s}(\Gamma)$ que dans l'espace classique $L^{2}(\Gamma)$ de mesure d'énergie.

Remarque 22   Ce genre de majoration dans l'espace de Sobolev $H^{-s}(\Gamma)$ avec s > 1/2 garde un intérêt pratique. En effet, l'amplitude de diffusion, importante pour les applications (entre autres le calcul de la Section Efficace Radar (aussi appelée Surface Equivalente Radar), section I.4.2), notée $a(\theta)$, est obtenue à l'aide de (I.3.27).

$$\null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil$... ...{\nu} \, \vec{e}_{\theta} u + \partial_{\nu} u)} \cr \crcr}}\,$$ (I.3.13)

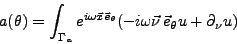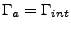
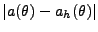
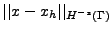
On prend $\Gamma_a = \Gamma_{int}$ la frontière de l'objet diffractant, et on utilise la majoration (I.3.36) du lemme 9. On majore alors $\vert a(\theta)-a_h(\theta)\vert$ par $\vert\vert x-x_h\vert\vert _{H^{-s}(\Gamma)}$ grâce à l'inégalité de Cauchy-Schwarz.