




suivant: II.10.2.2 Intérêt par rapport à une méthode
monter: II.10.2 Utilisation optimale.
précédent: II.10.2 Utilisation optimale.
Table des matières
Index
II.10.2.1 Un cas hors de portée des méthodes classiques.
On s'intéresse au cas modèle du cube II.10.1 a) dans le vide avec L=60 centimètres. On utilise un maillage structuré en 8 hexaèdres à la fréquence de
1000 MHz. Nous effectuons deux calculs, pour deux incidences différentes:  et
et 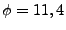 , puis
, puis 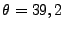 et
et  . Le tableau II.10.9) indique les caractéristiques du cas traité pour la première incidence. Nous choisissons,
. Le tableau II.10.9) indique les caractéristiques du cas traité pour la première incidence. Nous choisissons,
- soit, des directions constantes sur les 8 éléments,
- soit, de prendre des fonctions de base différentes sur les 8 éléments hexaédriques de façon à ne pas
privilégier une direction particulière pour l'ensemble du problème discret,
Dans le deuxième cas, on utilise toujours une loi de répartition aléatoire uniforme des directions de propagation à partir d'une
situation de référence qui dépend du nombre de fonctions choisies (cf section II.8.3).
Tableau II.10.9:
Simulation avec des hexaèdres réguliers d'arête la longueur d'onde.
|
<I>k0 |
(-0,322 ; -0.065 ; -0.944) |
polarisation |
TM |
|
<I>E0 |
(-0.925 ; -0.187 ; 0.329) |
 |
(19,2 ; 11,4) |
| p |
de 3 à 70 (aléatoires) |
K |
8 |
| f |
1 GHz |
 |
0,3 m |
| h |
0,3 m |
 |
1 |
Le maillage est extrêmement grossier puisque les arêtes des cubes du maillage ont comme longueur la longueur d'onde du problème. Un tel
problème n'est pas abordable pour une méthode classique d'éléments finis. Rappelons, que dans la méthode des éléments finis, on calcule h comme le plus grand des diamètres des éléments. Comme le diamètre d'un cube est  fois son arête, la méthode des éléments finis, sur ce calcul, indiquerait
fois son arête, la méthode des éléments finis, sur ce calcul, indiquerait
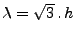 , et non
, et non 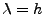 . Nous n'avons pas inclus d'objet diffractant de façon à connaître la solution analytique exacte du problème,
mais les résultats seraient semblables dans le cas par exemple d'un cube diffractant.
. Nous n'avons pas inclus d'objet diffractant de façon à connaître la solution analytique exacte du problème,
mais les résultats seraient semblables dans le cas par exemple d'un cube diffractant.
Figure II.10.22:
Evolution de l'erreur de bord pour des grosses mailles
|
La figure II.10.22 donne,
pour les deux incidences et les deux choix des directions, l'évolution,
en fonction du nombre de directions de propagation par élément,
de la norme
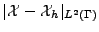 entre la solution approchée calculée par
entre la solution approchée calculée par
 et la solution exacte
et la solution exacte
 où <I>E et <I>H sont donnés par (II.10.3). L'annexe III.B.3 explique ce calcul.
où <I>E et <I>H sont donnés par (II.10.3). L'annexe III.B.3 explique ce calcul.
Dans le cas d'une diffraction sur un objet, la SER est liée à la norme
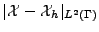 (cf section II.10.1.3).
Par exemple, une erreur de 10 % sur la norme de l'erreur équivaut à une erreur de 1 dB.m2 sur la SER par
(cf section II.10.1.3).
Par exemple, une erreur de 10 % sur la norme de l'erreur équivaut à une erreur de 1 dB.m2 sur la SER par
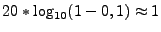 . Nous constatons que
. Nous constatons que
- Le code
 converge toujours, quel que soit le nombre de directions.
converge toujours, quel que soit le nombre de directions.
- Le nombre d'itérations nécessaires pour résoudre le système linéaire est très faible, la précision du calcul étant de toute façon assez faible.
- Il faut au moins 45 directions par élément pour obtenir une erreur inférieure à 10 %, au moins 35 pour une erreur inférieure à 30 % (qui donnerait approximativement
3 dB.m2 d'écart par rapport à la solution exacte.
- Le choix des directions est important pour obtenir une précision suffisante: ceci se voit à l'allure non monotone de la courbe II.10.22. Les résultats
sont globalement meilleurs pour des directions de propagation plus équiréparties (cf section II.8.3). Ainsi, le calcul avec 12 directions est meilleur qu'avec 14 moins
bien réparties sur la sphère unité. On observe surtout que le choix des directions aléatoires d'un élément à un autre, donne, en général, une erreur plus faible que le choix de directions toutes identiques. Ceci peut s'expliquer par l'anisotropie plus forte induite par le choix de directions constantes sur tous les éléments du maillage, alors que le choix de directions variables corrige globalement ce phénomène.
- Pour p directions par élément, le stockage est proportionnel à p(p+1)+12p2 et au nombre d'éléments du maillage (pour des hexaèdres). Pour 70 directions cela donne 63770 (unités de stockage)
alors que pour 7 on a 644 soit 99 fois moins. Par comparaison, une méthode d'éléments finis P1 pour un maillage en
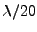 , utilise
, utilise
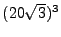 fois plus d'éléments, soit 42000
(et donc
fois plus d'éléments, soit 42000
(et donc 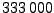 éléments au total). Dans une méthode d'éléments finis d'arête le stockage est proportionnel à
éléments au total). Dans une méthode d'éléments finis d'arête le stockage est proportionnel à
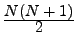 où N est le nombre d'arêtes de l'élément.
Sur des hexaèdres, le stockage sera donc proportionnel à 78 fois le nombre d'éléments. Dans une telle situation, le stockage pour la méthode éléments finis serait de 26 millions de termes dans la matrice du système linéaire, soit un stockage 50 fois supérieur à celui atteint par
où N est le nombre d'arêtes de l'élément.
Sur des hexaèdres, le stockage sera donc proportionnel à 78 fois le nombre d'éléments. Dans une telle situation, le stockage pour la méthode éléments finis serait de 26 millions de termes dans la matrice du système linéaire, soit un stockage 50 fois supérieur à celui atteint par
 pour 70 fonctions de base par élément. Dans le cas de l'utilisation de 35 directions de propagation
pour
pour 70 fonctions de base par élément. Dans le cas de l'utilisation de 35 directions de propagation
pour
 et d'un maillage en
et d'un maillage en 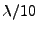 pour une méthode éléments finis, le stockage demandé par
pour une méthode éléments finis, le stockage demandé par
 sera 25 fois inférieur à celui demandé par la méthode des éléments
finis.
sera 25 fois inférieur à celui demandé par la méthode des éléments
finis.





suivant: II.10.2.2 Intérêt par rapport à une méthode
monter: II.10.2 Utilisation optimale.
précédent: II.10.2 Utilisation optimale.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() et
et ![]() , puis
, puis ![]() et
et ![]() . Le tableau II.10.9) indique les caractéristiques du cas traité pour la première incidence. Nous choisissons,
. Le tableau II.10.9) indique les caractéristiques du cas traité pour la première incidence. Nous choisissons,
![]() fois son arête, la méthode des éléments finis, sur ce calcul, indiquerait
fois son arête, la méthode des éléments finis, sur ce calcul, indiquerait
![]() , et non
, et non ![]() . Nous n'avons pas inclus d'objet diffractant de façon à connaître la solution analytique exacte du problème,
mais les résultats seraient semblables dans le cas par exemple d'un cube diffractant.
. Nous n'avons pas inclus d'objet diffractant de façon à connaître la solution analytique exacte du problème,
mais les résultats seraient semblables dans le cas par exemple d'un cube diffractant.
![]() (cf section II.10.1.3).
Par exemple, une erreur de 10 % sur la norme de l'erreur équivaut à une erreur de 1 dB.m2 sur la SER par
(cf section II.10.1.3).
Par exemple, une erreur de 10 % sur la norme de l'erreur équivaut à une erreur de 1 dB.m2 sur la SER par
![]() . Nous constatons que
. Nous constatons que
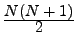 où N est le nombre d'arêtes de l'élément.
Sur des hexaèdres, le stockage sera donc proportionnel à 78 fois le nombre d'éléments. Dans une telle situation, le stockage pour la méthode éléments finis serait de 26 millions de termes dans la matrice du système linéaire, soit un stockage 50 fois supérieur à celui atteint par
où N est le nombre d'arêtes de l'élément.
Sur des hexaèdres, le stockage sera donc proportionnel à 78 fois le nombre d'éléments. Dans une telle situation, le stockage pour la méthode éléments finis serait de 26 millions de termes dans la matrice du système linéaire, soit un stockage 50 fois supérieur à celui atteint par