I.2.1.3 Construction de Galerkin de l'espace V_h.

Dans chaque élément $\Omega _k$, nous considérons un nombre fini de fonctions e_kl solutions indépendantes de l'équation de Helmholtz homogène dans l'élément $\Omega _k$. Un ensemble particulier de fonctions e_kl est celui des fonctions de support contenu dans $\Omega _k$:

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...omega^2)(e_{kl})_{\vert\Omega_k} = 0 \ . \cr \crcr}}\, \right.$$ (I.2.5)

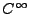L'utilisation de fonctions à support compact, comme cela est habituel dans la méthode des Eléments Finis, mène à un système dont la matrice est creuse. Remarquons que les fonctions e_kl ne sont pas continues sur $\Omega$ mais qu'elles sont $C^{\infty}$ sur l'intérieur strict de $\Omega _k$.

L'indice k (variant de 1 à K le nombre total de mailles) désigne le numéro de la maille dans laquelle e_kl n'est pas identiquement nulle. Le deuxième indice l correspond au numéro d'une fonction de base pour la maille $\Omega _k$: c'est une numérotation locale à la maille $\Omega _k$. Pour simplifier, nous prendrons un nombre constant, noté p, de fonctions de base pour toute maille $\Omega _k$. Les fonctions z_kl sont définies de façon univoque par $z_{kl}=(-\partial_{\nu_k}+i\omega ) e_{kl}$, e_kl étant une solution du système (I.2.7). Nous avons donc:

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ... (-\partial_{\nu_k} +i\omega )e_{kl} \ . \cr \crcr}}\, \right.$$ (I.2.6)

On vérifie que {z_kl}_k,l est une base de V_h sous les hypothèses du lemme suivant:

Lemme 3   La famille de fonctions 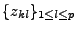$\{z_{kl}\}_{1 \leq l \leq p}$ définies par (I.2.8) est libre dans V si et seulement si la famille de fonctions $\{e_{kl}\}_{1 \leq l \leq p}$ est libre dans H_k.

On construit finalement l'espace discret V_h comme l'espace vectoriel engendré par les fonctions z_kl, autrement dit:

$$V_h = \mbox{ Vect } (z_{kl})_{1 \le k \le K}^{1 \le l \le p} \ .$$ (I.2.7)

On cherche donc la solution approchée x_h sous la forme d'une combinaison linéaire des fonctions de base: la solution approchée x_h est entièrement définie par la donnée des pK coefficients complexes x_kl définissant $X = (x_{kl})_{1 \le k \le K}^{1 \le l \le p}$ tels que

$$(x_h)_{\vert\partial \Omega_k} = \sum_{l=1}^{p}{x_{kl} \, z_{kl}} \ ,$$ (I.2.8)

ou exprimée en fonction des e_kl:

$$(x_h)_{\vert\partial \Omega_k} = \sum_{l=1}^{p}{x_{kl}(-\partial_{\nu_k} +i\omega )e_{kl}} \ .$$ (I.2.9)