




suivant: III.D.2.2 Programmation de I2.
monter: III.D.2 Algorithmes conditionnels de programmation.
précédent: III.D.2 Algorithmes conditionnels de programmation.
Table des matières
Index
III.D.2.1 Programmation de I1.
Rappelons que I1 est donné par
|
(III.D.9) |
 |
Cette fonction dont le domaine de définition est
 admet une limite pour
admet une limite pour  tendant vers 0,
tendant vers 0,
ce qui permet de donner un sens à I1(0). En revanche, un ordinateur, quel qu'il soit, ne peut calculer I1(0) par la formule (III.D.9) puisque la division par zéro
est interdite. La notion de limite, ou de prolongement par continuité, est une notion formelle que le calculateur ignore. En revanche, pour tous les autres décimaux (qui sont en nombre fini) connus par la machine,
on pourra calculer la fonction I1. En effet, il existe un nombre, que l'on note  , qui est le plus petit réel (en fait décimal) strictement positif de la machine. Pour ce nombre, et tous
les nombres dont la valeur absolue est supérieure, le calculateur peut effectuer la division. La fonction
, qui est le plus petit réel (en fait décimal) strictement positif de la machine. Pour ce nombre, et tous
les nombres dont la valeur absolue est supérieure, le calculateur peut effectuer la division. La fonction  est approchée par son développement limité à un ordre qui dépend du
calculateur. Par exemple,
est approchée par son développement limité à un ordre qui dépend du
calculateur. Par exemple,  sera approché par la fonction polynômiale
sera approché par la fonction polynômiale

Pour
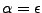 , le nombre
, le nombre  n'existe pas dans la machine puisqu'il est compris entre
n'existe pas dans la machine puisqu'il est compris entre  et 0 (pour
et 0 (pour
 , ce qui est évidemment le cas, le contraire ne
se conçoit pas). Pour
, ce qui est évidemment le cas, le contraire ne
se conçoit pas). Pour  assez petit, le calculateur remplacera
assez petit, le calculateur remplacera  par sa valeur approchée la plus proche, soit 0. On aura doncIII.D1
par sa valeur approchée la plus proche, soit 0. On aura doncIII.D1
La division de  par
par  rend alors 1 le nombre entier naturel représenté par le décimal
rend alors 1 le nombre entier naturel représenté par le décimal  ou en binaire par la mantisse
ou en binaire par la mantisse  et l'exposant
et l'exposant  (le nombre de zéros dépend de la précision du calculateur, ou mode de représentation des réels). Nous en tirons les conclusions suivantes:
(le nombre de zéros dépend de la précision du calculateur, ou mode de représentation des réels). Nous en tirons les conclusions suivantes:
- l'erreur effectuée par le calculateur sur la fonction sinus cardinale est donc de l'ordre de
 donc inférieure à
donc inférieure à  et non quantifiable,
et non quantifiable,
- il est inutile de calculer
 par la formule (III.D.9) puisque
par la formule (III.D.9) puisque
 pour le calculateur.
pour le calculateur.
Cherchons à prolonger notre raisonnement sur le calcul de  à des nombres plus grands. La question est de savoir à partir de quel nombre
à des nombres plus grands. La question est de savoir à partir de quel nombre  la calculateur fera la différence
entre 1 et le sinus cardinal de
la calculateur fera la différence
entre 1 et le sinus cardinal de  . En informatique, on définit un nombre, que nous noterons pm, appelé la ``précision machine'' qui est le plus grand réel positif tel que le test
``le réel 1 plus la précision machine est égal au réel 1'' soit vrai. On peut aussi le définir par le plus petit réel positif tel que le test ``le réel 1 plus la précision machine
est égal au réel 1'' soit faux. La différence entre ces deux définitions est
. En informatique, on définit un nombre, que nous noterons pm, appelé la ``précision machine'' qui est le plus grand réel positif tel que le test
``le réel 1 plus la précision machine est égal au réel 1'' soit vrai. On peut aussi le définir par le plus petit réel positif tel que le test ``le réel 1 plus la précision machine
est égal au réel 1'' soit faux. La différence entre ces deux définitions est  et évidemment (pour tout calculateur à exposant)
et évidemment (pour tout calculateur à exposant)  est très petit devant pm.
Nous cherchons donc
est très petit devant pm.
Nous cherchons donc  le plus grand réel positif tel que
le plus grand réel positif tel que
Toujours dans le cas où la fonction sinus est connue par son développement à l'ordre 4 (ou 5),  vérifie
vérifie
Lorsque le calculateur approche la fonction sinus à un ordre plus élevé et que la précision machine est assez petite devant 1, on peut toujours approcher  par
par  .
Par exemple, à l'ordre 6, on aura
.
Par exemple, à l'ordre 6, on aura
approximativement vérifié par
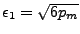 à 0,3 pm2 (près), donc à 0,3 pm par rapport à pm (en erreur relative). Cette différence (par définition de pm)
n'est pas représentée par la machine (donne le même nombre
à 0,3 pm2 (près), donc à 0,3 pm par rapport à pm (en erreur relative). Cette différence (par définition de pm)
n'est pas représentée par la machine (donne le même nombre  ). Nous proposons donc l'algorithme de calcul suivant:
). Nous proposons donc l'algorithme de calcul suivant:
- définition de
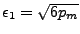 ,
,
- pour tout
 ,
,
La fonction  est ainsi calculée à la précision
est ainsi calculée à la précision
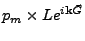 en un nombre minimal d'opérations. L'erreur relative sur I1 est donc de l'ordre de la
précision machine, précision maximale inhérente au calculateur.
en un nombre minimal d'opérations. L'erreur relative sur I1 est donc de l'ordre de la
précision machine, précision maximale inhérente au calculateur.





suivant: III.D.2.2 Programmation de I2.
monter: III.D.2 Algorithmes conditionnels de programmation.
précédent: III.D.2 Algorithmes conditionnels de programmation.
Table des matières
Index
Cessenat Olivier
2007-04-21