suivant: I.5.1.3 Propriétés de la formulation.
monter: I.5.1 Présentation du problème et formulation.
précédent: I.5.1.1 Cadre du problème.
Table des matières
Index
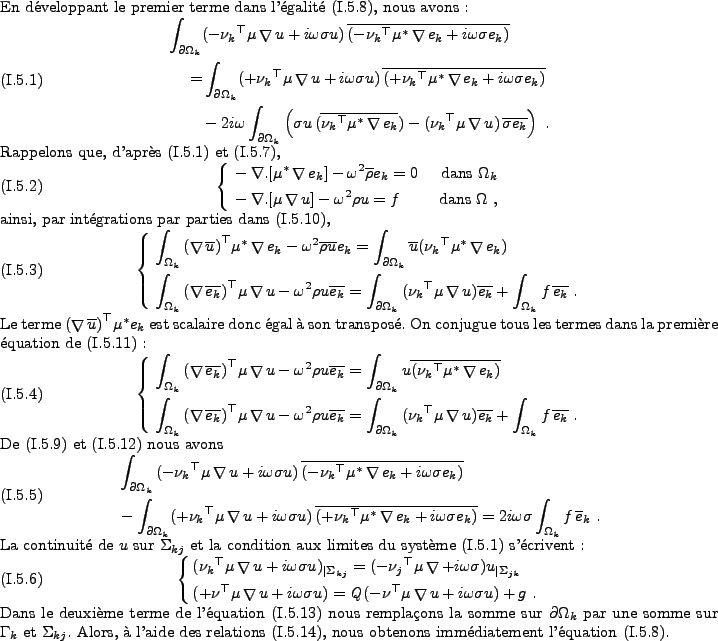
Comme pour le problème sans coefficient, nous définissons les opérateurs E, F,  et A.
et A.
Notons F* l'adjoint de F. Définissons l'opérateur A de V dans V par
|
(I.5.12) |
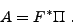 |
On a de la même façon que pour le problème sans coefficient le théorème d'existence et d'unicité suivant. Les arguments des preuves sont identiques.





suivant: I.5.1.3 Propriétés de la formulation.
monter: I.5.1 Présentation du problème et formulation.
précédent: I.5.1.1 Cadre du problème.
Table des matières
Index
Cessenat Olivier
2007-04-21
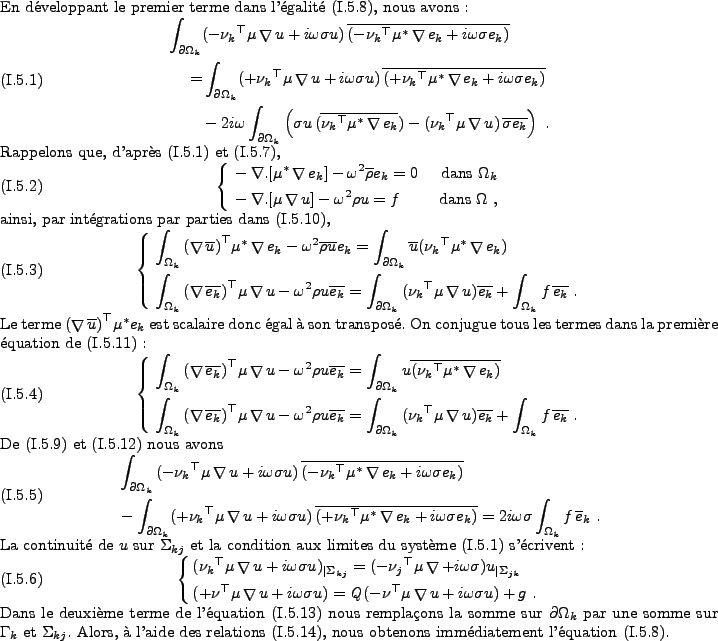
![]() et A.
et A.