II.10.1.3 Notion de SER.

On définit la SER rétro-diffusée dans la direction v par

$$% SER = 10 * \log_{10} \left( \frac{\displaystyle \omega^2}{\displaystyle 32\pi} \vert a\vert^2 \right)$$ (II.10.7)

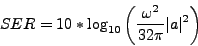où l'amplitude de diffusion a est donnée par

(II.10.8) html_comment_mark> |a|²=|a_<I>F^h|²+|a_<I>G^h|²

pour

$$a_{{{\mathbf F}}}^h = \int_{\Gamma} \left( \left( {{\mathbf ... ...( \left( {{\mathbf H}}_h \wedge \nu \right) \wedge \nu \right)$$ (II.10.9)

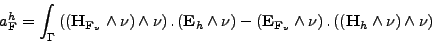(et de même pour a_<I>G^h en remplaçant (<I>E_<I>Fv,<I>H_<I>Fv) par (<I>E_<I>Gv,<I>H_<I>Gv)) avec

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...= -i {{\mathbf E}}_{{{\mathbf G}}_v} \ , \cr \crcr}}\, \right.$$ (II.10.10)

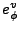où le vecteur v=e^v_r définit les polarisations $e^v_{\theta}$ et $e^v_{\phi}$ dans un repère sphérique (cf [7]).

La frontière $\Gamma$ de calcul de la SER est n'importe quelle surface incluant l'objet diffractant et placée dans le vide.

Remarque 46   Le fait que $\Gamma$ soit dans le vide indique que l'on peut

• calculer la SER sur la frontière artificielle car elle est toujours placée dans le vide par hypothèse,
• calculer la SER sur deux frontières à savoir la frontière de l'objet décrite par les faces $\Sigma_{k,k}$ là où il n'est pas recouvert de matériau, et l'interface vide/matériau. Cette interface est décrite par les faces $\Sigma_{k,j}$ telle que $\Omega_{k}$ soit dans le vide et $\Omega_{j}$ possède un matériau. Ceci exclut l'éventualité d'un nuage dans le domaine de calcul.

Pour des raisons de précision numérique il est traditionnel d'effectuer le calcul de la SER sur la surface dans le vide la plus proche possible de l'objet, ce qui correspond à la deuxième situation.

On montre que le calcul de la SER, comme le calcul d'erreur par rapport à une solution exacte qui serait une onde plane, est de la même complexité que le calcul des termes matriciels pour la contribution du bord $\Gamma$ du domaine $\Omega$. Nous ne développerons pas ces calculs. Notons simplement que, pour,

$$\null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil$... ...heta}-ie^v_{\phi}) e^{-i\omega \vec{y}e^v_r} \ , \cr \crcr}}\,$$ (II.10.11)

la contribution des faces de bord pour l'amplitude de diffusion est donnée par les formules

$$\null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil$\... ...ight) \wedge \nu_{k} \right)} . \left( g \right) \cr \crcr}}\,$$

et

$$\null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\strut\hfil$\... ...) \wedge \nu_{k} \right)} . \left( g \right) \ . \cr \crcr}}\,$$

Un calcul similaire montre que la contribution des interfaces internes entre des éléments $\Omega _k$ dans le vide et $\Omega_j$ quelconque, s'obtient aussi comme des calculs de termes du système linéaire par des couplages des fonctions de base avec les fonctions <I>F_-v et <I>G_-v qui ne dépendent que de la direction d'observation.