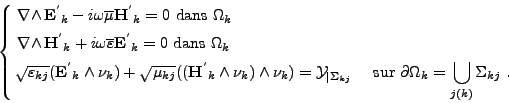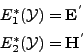Nous définissons pour Maxwell les opérateurs équivalents á ceux définis lors de l'étude du problème de Helmholtz. Nous supposons toujours les coefficients ![]() et
et ![]() constants
sur les éléments à frontière lipschitzienne de la partition de
constants
sur les éléments à frontière lipschitzienne de la partition de ![]() effectuée section II.7.2.1.
effectuée section II.7.2.1.
| (II.7.62) | 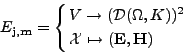 |
![[*]](crossref.gif) ).
).