




suivant: III.D.1 Formules analytiques des intégrales d'ondes planes.
monter: 3 Annexes
précédent: III.C.5 Code Maxwell tridimensionnel avec ou sans
Table des matières
Index
III.D Calcul des termes intégraux du système linéaire.
Dans ce chapitre nous nous intéressons au calcul de l'intégrale de la fonction
sur un segment [x1,x2], un triangle [x1,x2,x3] et un tétraèdre
[x1,x2,x3,x4]. Les fonctions intégrales sont respectivement I1, I2 et I3. Le calcul de cette intégrale est
en effet nécessaire pour formuler les termes du système linéaire, puisque les fonctions de base du problème variationnel sont des ondes planes, que ce soit pour le problème de Helmholtz ou
pour le problème de Maxwell. Le calcul simple des formules est effectué dans la section III.D.1. Les trois fonctions I1, I2 et I3 ne sont pas définies sur
respectivement  ,
,
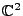 et
et
 ce qui interdit d'inclure directement les formules analytiques de calcul dans un programme (pour ordinateur). En revanche, comme ces fonctions se prolongent par
des fonctions continues (sur respectivement
ce qui interdit d'inclure directement les formules analytiques de calcul dans un programme (pour ordinateur). En revanche, comme ces fonctions se prolongent par
des fonctions continues (sur respectivement  ,
,
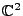 et
et
 ), il est possible d'implémenter le calcul à l'aide de tests judicieux pour maximiser la précision du résultat. Ce travail,
qui consiste notamment à effectuer les développements limités adéquats, est présenté section III.D.2. Le lecteur averti sait que cette recette de programmation
limite les performances d'une machine à architecture vectorielle. Nous présentons section III.D.3 comment opérer la vectorisation à moindre coût. Ce travail consiste
à utiliser certaines fonctions intrinsèques dont la vectorisation est complète sur le calculateur.
), il est possible d'implémenter le calcul à l'aide de tests judicieux pour maximiser la précision du résultat. Ce travail,
qui consiste notamment à effectuer les développements limités adéquats, est présenté section III.D.2. Le lecteur averti sait que cette recette de programmation
limite les performances d'une machine à architecture vectorielle. Nous présentons section III.D.3 comment opérer la vectorisation à moindre coût. Ce travail consiste
à utiliser certaines fonctions intrinsèques dont la vectorisation est complète sur le calculateur.
Sous-sections





suivant: III.D.1 Formules analytiques des intégrales d'ondes planes.
monter: 3 Annexes
précédent: III.C.5 Code Maxwell tridimensionnel avec ou sans
Table des matières
Index
Cessenat Olivier
2007-04-21