I.3.1 Notion d'ordre de convergence et rappels sur la méthode des éléments finis.

Soit un domaine bidimensionnel $\Omega$ borné. La théorie classique (cf [17]) des éléments finis montre que si l'on discrétise le problème

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...} \Omega \cr & u=0 & \mbox{ sur } \Gamma \cr \crcr}}\, \right.$$

à l'aide d'éléments finis P_k, on obtient l'estimation^I.31 suivante, si $u \in H^{k+1}(\Omega)$ avec $k+1 \geq m$ (cf [54]), alors

$$\vert\vert u-u_h\vert\vert _{H^{m}(\Omega)} \leq C h^{k+1-m} \vert\vert u\vert\vert _{H^{k+1}(\Omega)} \ .$$

Dans l'inégalité ci-dessus, h est le paramètre de raffinement du maillage (que l'on suppose régulier, vérifiant les hypothèses H1, H2 et H3 section I.2.1.2). L'exposant de h est ce que l'on appelle l'ordre de la méthode. Par exemple, pour k=1, on a

$$\vert\vert u-u_h\vert\vert _{L^2(\Omega)} \leq C h^{2} \vert\vert u\vert\vert _{H^{2}(\Omega)} \ .$$

Pour k=2, on a

$$\vert\vert u-u_h\vert\vert _{L^2(\Omega)} \leq C h^{3} \vert\vert u\vert\vert _{H^{3}(\Omega)} \ .$$

Comme dans la méthode des Eléments Finis (FEM) nous dirons que la méthode est d'ordre $n \in {\mathbb{N}}$ si, pour toute solution régulière, il existe une constante positive C telle que, pour une norme sur le bord $\Gamma$,

$$\vert\vert x-x_h\vert\vert _{\Gamma} \leq C h^{n}$$

où x_h est défini par (I.2.15) et x par (I.0.8). Nous avons réalisé des tests numériques afin d'étudier l'ordre de convergence dans d'autres normes telles que ||x-x_h||_V, $\vert\vert u-u_h\vert\vert _{\Gamma}$ et $\vert\vert u-u_h\vert\vert _{\Omega}$ section I.3.2. Les estimations théoriques effectuées dans ce chapitre porteront sur des estimations L² ou H^-s avec s > 1/2: nous supposerons donc que $\Gamma$ est Lipschitz continue par morceaux.

L'ordre de convergence permet d'estimer asymptotiquement l'erreur en fonction de k et h. Nous sommes d'autre part en mesure de comparer les évolutions de la place mémoire et du temps de calcul entre la FEM et la formulation UWVF.

Prenons un exemple précis. Soit $\cal {C}$ un carré de base unitaire maillé par une triangulation structurée. Le maillage est constitué de 2n² éléments. Dans cette section, on définit le paramètre de raffinement du maillage h par h=1/n: c'est la longueur des côtés des triangles dans les deux directions d'axes^I.31. Il y a (n+1)² nuds, 4n arêtes libres, 3n²-2n interfaces, donc, au total, 3n²+2n arêtes. La figure I.3.1 donne le maillage de $\cal {C}$.

Figure I.3.1: Maillage de $\cal {C}$.

Le nombre de degrés de liberté dans la FEM par des éléments P₁, c'est-à-dire par des fonctions centrées aux nuds, est exactement le nombre de nuds (n+1)² si l'espace d'approximation est $H^1(\cal{C})$, ou le nombre de nuds internes (n-1)² si l'espace d'approximation est $H^1_0(\cal{C})$ (lorsque l'on traite d'un problème de Dirichlet). Considérant des éléments P₂, on rajoute les fonctions dont les supports sont localisés sur les milieux des arêtes. Ces fonctions sont au nombre de 3n²+2n pour $H^1(\cal{C})$ et 3n²-2n moins le nombre d'interfaces ayant un nud à la frontière (8n-6) pour $H^1_0(\cal{C})$, totalisant 4n²+4n+1 et 4n²-12n+7 respectivement.

Dans un contexte plus général, si l'on prend des éléments finis P_k sur la triangulation ci-dessus, le nombre de degrés de liberté de l'espace d'approximation V_h de $H^1(\cal{C})$ est (n+1)² le nombre de nuds, plus (k-1) fois le nombre d'arêtes (3n²+2n) plus le nombre d'éléments du maillage (2n²) fois la dimension de P_k qui est $\frac{\displaystyle (k+2)(k+1)}{\displaystyle 2}$ (cf [54]) moins 3k qui est le nombre de nuds des arêtes d'un triangle. 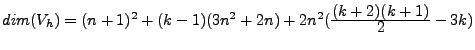On a donc $dim(V_h)=(n+1)^2+(k-1)(3n^2+2n)+2n^2(\frac{\displaystyle (k+2)(k+1)}{\displaystyle 2}-3k)$ soit dim(V_h)=n²k²+2nk+1. Comptons maintenant le nombre d'éléments non nuls de la matrice du système linéaire en considérant la matrice ligne par ligne. Les éléments non nuls pour une ligne numéro q proviennent des couplages entre la fonction numéro q de V_h et ses fonctions voisines, c'est-à-dire les fonctions ayant un support d'intersection non vide avec le support de la q-ième fonction de base. Pour des éléments P₁, ceci est équivalent à compter le nombre de nuds voisins, qui est de 6 pour un nud interne, ce qui est le cas pour la plupart des nuds. Pour des éléments P₂, ceci revient, pour chaque triangle, à compter les nuds voisins et les nuds milieux de chaque segment jusqu'à trois points. Si l'on considère une fonction à l'intérieur du domaine (ce qui représente la plupart des fonctions), on dénombre 36 nuds voisins. Pour P₃, on a 90 fonctions à coupler. Ceci augmente avec k comme 2(2k)²-2+(2k-2)(2k-1)=12k²-6k. Le stockage est équivalent (il est en réalité légèrement inférieur à cause des nuds proches de la frontière) à $(12k^2-6k)(n^2k^2+2nk+1)=12\,{n}^{2}{k}^{4}+24\,n{k}^{3}-6\,{n}^{2}{k}^{3}+12\,{k}^{2}-12\,n{k} ^{2}-6\,k$. Pour des Eléments Finis P₁, en considérant un grand nombre n, le stockage se comporte en 6n². Pour des EF P₂, en 144n², et enfin pour des EF P₃ en 810n². La FEM a donc les caractéristiques suivantes

Tableau I.3.1: FEM

éléments	n uds	interfaces	arêtes libres	arêtes
2n2	(n+1)2	3n2-2n	4n	3n2+2n
Type d'éléments finis	P1	P2	P3	Pk
Degrés de Liberté des EF	(n+1)2	4n2+4n+1	9n2+6n+1	n2k2+2nk+1
Erreur	n-2	n-3	n-4	n-(k+1)
Couplage de fonctions de base	6	36	90	12k2-6k
Stockage	6(n+1)2	36(4n2+4n+1)	$\approx 810n^2$	$\approx 6 n^2k^3(2k-1)$

Dans la méthode UWVF, le nombre de degrés de liberté est le nombre de fonctions de base par élément (noté p) fois le nombre d'éléments 2n² (si l'on en prend un nombre constant de fonctions de base par élément). Le stockage est donné par le couplage hermitien des fonctions de base sur chaque élément n²p(p+1), les couplages sur les 3n²-2n interfaces du maillage, i.e. (3n²-2n)p², et enfin par le couplage non hermitien des fonctions de base aux arêtes libres, ce qui rajoute 2np(p-1) termes. Ceci totalise $2n^2((p+1)(p)/2+3p^2)-2np \approx 7n^2p^2$ unités de stockage. Nous voyons section I.3.3.5 par (I.3.67) que l'erreur sur $\vert\vert u-u_h\vert\vert _{L^2(\Gamma)}$ se comporte en $h^{[(p-1)/2]-1/2} \vert\vert u\vert\vert _{C^{[(p+1)]/2}(\Omega)}$.

Les comparaisons asymptotiques de la taille mémoire et de l'ordre de convergence entre la méthode UWVF et la méthode FEM sont résumées dans le tableau (I.3.2)^I.31.

Tableau I.3.2: Comparaison UWVF-FEM

Méthode	FEM (k)	UWVF (p)
Ordre de l'erreur	(k+1)	-1/2+[(p-1)/2]
Stockage	12n2k4	7n2p2
Degrés de Liberté	n2k2	2n2p

Remarque 12   Les estimations pour la FEM sont données pour des normes sur le domaine entier $\Omega$, alors que pour la méthode UWVF nous ne donnons d'estimation que sur la frontière $\Gamma$. C'est pourquoi les ordres en norme $L^{2}(\Omega)$ et en norme $L^{2}(\Gamma)$ diffèrent de 1/2. D'autre part, rappelons que l'ordre donné pour la méthode UWVF dans le tableau (I.3.2) est l'ordre théorique démontré dans ce chapitre: cet ordre n'est pas optimal, l'ordre numérique observé est la fonction

$$+1/2+[(p-1)/2] \ .$$

Cette loi numérique montre l'intérêt de la méthode pour p petit.

Remarque 13   Le tableau (I.3.2) met en lumière le fait que le même taux de précision peut être atteint en utilisant la méthode UWVF à la place de la FEM pour un stockage informatique réduit. Il en est de même du temps de calcul. Ceci provient du fait que la méthode UWVF est une méthode d'ordre asymptotiquement plus élevé que la FEM au sens où l'ordre de convergence est en racine carrée du stockage dans la méthode UWVF au lieu de la racine quatrième du stockage pour la FEM.