II.8.2.2 Construction d'un espace d'approximation particulier.

Nous avons alors choisi de construire notre espace d'approximation V_h à partir 

i)

d'une partition de $\Omega$ en K éléments réguliers $\Omega _k$ soit tétraédriques soit hexaédriques. Notons que ce maillage définit l'espace fonctionnel ``continu'' V de la formulation variationnelle ultra-faible (II.7.84). La terminologie ``éléments réguliers'' signifie que le maillage vérifie les hypothèses H1, H2 et H3 ([17]).

ii)

Sur chaque maille $\Omega _k$ on considère les p directions de propagation V_k,l^' vérifiant (II.8.20), l'indice l^' variant de 1 à p, et p vecteurs polarisation réels et normés <I>E⁰_k,l^' orthogonaux aux directions de propagation respectives. Ces vecteurs définissent les p fonctions de type <I>F, (<I>E^<I>F_k,l^',<I>H^<I>F_k,l^') ((II.8.22) et (II.8.25)) et les p fonctions associées de type <I>G, (<I>E^<I>G_k,l^',<I>E^<I>G_k,l^') ((II.8.23) et (II.8.26)).

Les fonctions de base ${{\mathcal{Z}}}_{kl}$ sont construites pour l variant de 1 à L=2p par les relations (II.8.5) à l'aide des fonctions (<I>E^'_kl,<I>H^'_kl)=(<I>E^<I>F_k,l,<I>H^<I>F_k,l) pour $1\le l \le p$ et des fonctions (<I>E^'_kl,<I>H^'_kl)=(<I>E^<I>G_k,l-p,<I>H^<I>G_k,l-p) pour $p+1\le l \le 2p$. On a donc

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...) } \cr & \mbox{ pour } 2p \ge l > p \ . \cr \crcr}}\, \right.$$ (II.8.29)

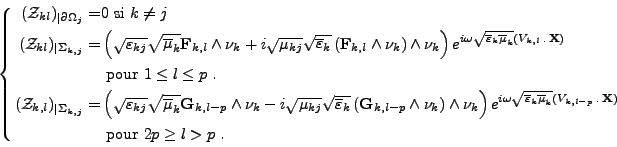Lemme 18   Les fonctions de base choisies sont bien indépendantes. En effet, d'après le lemme 17 la famille de fonctions analytiques sur $\Omega _k$, (<I>E^<I>F_k,l,<I>E^<I>G_k,l)_l=1,p, de cardinal 2p est linéairement indépendante sur $\Omega _k$ donc sur ${{\mathcal{H}}}(\Omega_k,\partial \Omega_k)$. Le lemme 15 montre alors que la famille $({{\mathcal{Z}}}_{kl})_{l=1,2p}$ est libre. Nous sommes donc dans le cadre des hypothèses du lemme 16 qui assure l'inversibilité de la matrice D du système linéaire discret (II.8.2).

Proposition 14   La donnée des p vecteurs réels <I>E⁰_k,l^' et V_k,l^' définit complètement les fonctions de base ${{\mathcal{Z}}}_{kl}$ et donc la matrice hermitienne de produit scalaire D_k par

$$D_k^{l,m} = ({{\mathcal{Z}}}_{km},{{\mathcal{Z}}}_{kl})_V \ .$$

Montrons que le déterminant de D_k ne dépend pas du choix des vecteurs <I>E⁰_k,l^' à partir d'une direction de propagation V_k,l^' fixée.

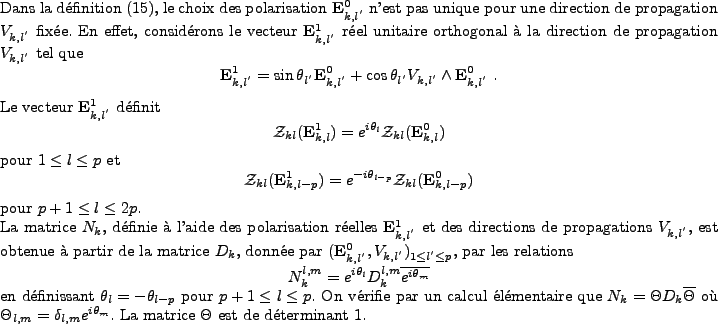
Remarque 38 (Sur le choix du maillage)   Comme pour le choix de l'espace pour le problème de Helmholtz, la partition proposée se réalise simplement à l'aide d'un mailleur. Notons que les éléments tétraédriques sont mieux adaptés que les hexaèdres pour mailler un objet quelconque. Nous proposons de fixer le type des éléments du maillage pour faciliter la mise en uvre informatique sur un ordinateur à architecture vectorielle. Notons en outre que l'utilisation d'éléments tétraédriques minimise les couplages entre éléments voisins, ce qui réduit à la fois la place mémoire informatique et le temps de calcul. Pour K éléments et L fonctions de base par élément, nous estimons sommairement que la taille mémoire nécessaire est proportionnelle à

$$K(L^2)N + K(\frac{\displaystyle L(L+1)}{\displaystyle 2})$$ (II.8.30)

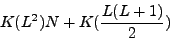où N est le nombre de faces par élément, N vaut 4 pour des tétraèdres, 5 pour des pentaèdres, 6 pour des hexaèdres. L'assemblage de la matrice est deux fois plus long sur une face à quatre sommets par rapport à une face à trois sommets. En outre une itération de l'algorithme itératif de résolution du système matriciel (I.2.39) demande $50\%$ de calculs en plus pour un maillage en hexaèdres que pour un maillage en tétraèdres (pour le même nombre d'éléments). Le nombre de degrés de libertés reste inchangé, égal à 2pK.

Remarque 39 (Sur le choix des fonctions de base)   Comme pour le problème de Helmholtz, le choix de fonctions de base issues d'ondes planes se justifie par le fait que les termes des matrices du système linéaire se calculent par des formules analytiques. Fixer le nombre de fonctions de base facilite la mise en uvre informatique sur un ordinateur à architecture vectorielle. L'utilisation de fonctions de bases identiques sur tous les éléments permet une amélioration du temps d'assemblage informatique des matrices du système linéaire, et éventuellement une réduction du stockage. De plus, nous exposons dans la section II.8.2.3 l'intérêt spécifique aux équations de Maxwell de choisir des fonctions de base issues de fonctions aux polarisations complexes conjuguées. Ce choix particulier permet de réduire au mieux la taille mémoire du système linéaire. Nous montrons, section II.8.2.3, que pour un problème dans le vide, la place mémoire du système linéaire est proportionnelle à

$$2K(p^2)N + K\left( p(p+1) \right)$$ (II.8.31)

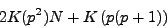au lieu de (II.8.30) pour L=2p, soit approximativement une division par deux de la place mémoire.