




suivant: III.D.2.3 Programmation de I3.
monter: III.D.2 Algorithmes conditionnels de programmation.
précédent: III.D.2.1 Programmation de I1.
Table des matières
Index
III.D.2.2 Programmation de I2.
La programmation de I2 est beaucoup plus compliquée que celle de I1, beaucoup de situations possibles sur les paramètres de calcul interviennent. Nous allons présenter au lecteur plusieurs
algorithmes possibles de calcul et pour l'un deux un résumé de la marche suivie pour minimiser l'erreur.
Rappelons que I2 est donné par
|
(III.D.10) |
 |
Le domaine de définition de
 est
est
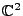 privé des droites
privé des droites
 ,
,  et
et  . On prolonge cette fonction par continuité sur
. On prolonge cette fonction par continuité sur
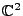 : la fonction prolongée est analytique sur
: la fonction prolongée est analytique sur
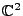 . Comme nous l'avons expliqué pour le calcul de
I1 (III.D.9), il n'est pas possible de calculer I2 directement sur le plan complexe puisque la division par zéro est interdite sur un calculateur. Nous allons
suivre la même démarche que pour le calcul de I1. On remarque que si l'on pose
. Comme nous l'avons expliqué pour le calcul de
I1 (III.D.9), il n'est pas possible de calculer I2 directement sur le plan complexe puisque la division par zéro est interdite sur un calculateur. Nous allons
suivre la même démarche que pour le calcul de I1. On remarque que si l'on pose
on calcule I2 par
Nous savons maintenant calculer la fonction  sur
sur  puisque c'est le même problème que celui du calcul de
puisque c'est le même problème que celui du calcul de  . Ceci implique que nous sommes capables de calculer
. Ceci implique que nous sommes capables de calculer
 sur les axes
sur les axes  et
et  . Le problème nouveau de notre étude est donc de calculer la fonction I2 dans un voisinage de la droite
. Le problème nouveau de notre étude est donc de calculer la fonction I2 dans un voisinage de la droite  à la meilleure précision possible et
avec le moins d'opérations possible. Le critère supplémentaire à considérer est donc
à la meilleure précision possible et
avec le moins d'opérations possible. Le critère supplémentaire à considérer est donc
 proche de zéro ou pas, et dans quel sens. En effet, on a,
proche de zéro ou pas, et dans quel sens. En effet, on a,
Lorsque  , la fonction
, la fonction
 tend vers
tend vers
au premier ordre, avec
La fonction dérivée  admet une limite en zéro. Nous pouvons donc proposer l'algorithme suivant.
Nous laissons au lecteur le soin de déterminer
admet une limite en zéro. Nous pouvons donc proposer l'algorithme suivant.
Nous laissons au lecteur le soin de déterminer 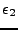 et
et  de façon à minimiser l'erreur globale du calcul. Pour cela, il faudra effectuer des estimations pointues des restes des
fonctions approchant I2.
de façon à minimiser l'erreur globale du calcul. Pour cela, il faudra effectuer des estimations pointues des restes des
fonctions approchant I2.
Nous avons préféré utiliser un autre algorithme qui exploite les propriétés particulières de la fonction
 issues de considérations géométriques. En effet, rappelons que
l'on a défini
issues de considérations géométriques. En effet, rappelons que
l'on a défini
 ,
,
 et
et
 . Si on
remplace
. Si on
remplace  par
par  et
et  par
par  , on sait que
, on sait que
La fonction
 est une alternative au calcul de I2 donné par la formule (III.D.10).
est une alternative au calcul de I2 donné par la formule (III.D.10).
Nous pouvons donc développer l'algorithme plus simple suivant.
- Si
 , un réel positif à définir que l'on suppose supérieur à
, un réel positif à définir que l'on suppose supérieur à  , alors nous avons le choix suivant.
, alors nous avons le choix suivant.
- Si
 , alors,
, alors,
- si
 , alors,
, alors,
- sinon,
- Si
 , alors on effectue un développement de Taylor par rapport à
, alors on effectue un développement de Taylor par rapport à  et
et  , et l'on peut calculer I2 par
, et l'on peut calculer I2 par
où
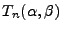 est le polynôme approchant le développement limité de la différence des deux sinus cardinaux de
est le polynôme approchant le développement limité de la différence des deux sinus cardinaux de  et
et  à l'ordre n-2 par rapport aux deux variables: n est l'ordre du développement de Taylor à effectuer sur la fonction I2.
Par exemple,
à l'ordre n-2 par rapport aux deux variables: n est l'ordre du développement de Taylor à effectuer sur la fonction I2.
Par exemple,
|
(III.D.11) |
 |
Notons que si l'on veut éviter le calcul et la multiplication par
 , on peut aussi calculer I2 par
, on peut aussi calculer I2 par
où
 est le polynôme approchant le développement limité de I2 à l'ordre n par rapport aux deux variables
est le polynôme approchant le développement limité de I2 à l'ordre n par rapport aux deux variables  et
et  . Par exemple,
. Par exemple,
|
(III.D.12) |
 |
- Si
 , alors,
, alors,
Il nous reste à choisir 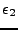 de façon à optimiser la précision du calcul de I2 puis à minimiser le nombre d'opérations à effectuer. Il s'agit d'étudier les précisions
des calculs de I2 par les différentes formules présentées, puis d'obtenir les mêmes précisions sur tous les cas limites afin que la majoration globale de l'erreur sur le calcul de I2 soit aussi faible que possible.
Sous l'hypothèse
de façon à optimiser la précision du calcul de I2 puis à minimiser le nombre d'opérations à effectuer. Il s'agit d'étudier les précisions
des calculs de I2 par les différentes formules présentées, puis d'obtenir les mêmes précisions sur tous les cas limites afin que la majoration globale de l'erreur sur le calcul de I2 soit aussi faible que possible.
Sous l'hypothèse
 , les différentes formules de calcul utilisent les trois fonctions suivantes:
, les différentes formules de calcul utilisent les trois fonctions suivantes:
- la fonction h(x,y)
|
(III.D.13) |
 |
définie sur
 et
et
 et
et
 ,
,
- la fonction g(x,y)
|
(III.D.14) |
 |
définie sur
 et
et
 ,
,
- la fonction d(x,y)
|
(III.D.15) |
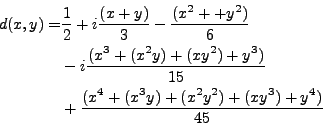 |
définie sur
 et
et
 .
.
La fonction d(x,y) permet d'approcher I2 en effectuant une erreur de l'ordre du premier terme oublié dans la série de Taylor, terme de la forme
dont le module est maximal pour 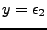 et
et  , et de valeur
, et de valeur
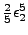 . Pour
. Pour 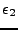 assez petit, nous ferons l'hypothèse que l'erreur est donc
assez petit, nous ferons l'hypothèse que l'erreur est donc
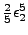 . Par exemple, pour
. Par exemple, pour
 , le terme suivant est 50 fois
inférieur à ce terme.
, le terme suivant est 50 fois
inférieur à ce terme.
Etudions comment se comporte la fonction g(x,y) (III.D.14) autour du point limite  et y=0. On a, puisque
et y=0. On a, puisque 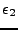 est petit,
est petit,
On constate que cette fonction a bien une limite informatique pour 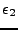 petit non nul et que cette limite est 1/2. En revanche, autour du point
petit non nul et que cette limite est 1/2. En revanche, autour du point
 et y=0, on a
et y=0, on a
Pour 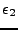 assez petit, l'ordinateur calcule 1-1 qui est nul, soit une erreur de l'ordre de 1/2, ce qui est inacceptable. L'erreur sur cette fonction de
assez petit, l'ordinateur calcule 1-1 qui est nul, soit une erreur de l'ordre de 1/2, ce qui est inacceptable. L'erreur sur cette fonction de 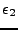 est
est
La même analyse peut être effectuée sur la fonction h(x,y) différence de deux fonctions évaluées à la précision machine et dont l'erreur sur la différence revient à étudier la
fonction g(x,y).
Nous choisissons donc 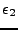 de façon à avoir
de façon à avoir
soit,
où l'on vérifie bien l'hypothèse
 à condition d'avoir
à condition d'avoir  .
L'erreur relative sur le calcul de I2 est alors majorée par
.
L'erreur relative sur le calcul de I2 est alors majorée par
pm5/6
qui est proche de la précision machine.
L'erreur effectuée sur le calcul de I2 est donc faible, largement inférieure à toute méthode de calcul par intégration numérique (sur des points de Gauss par exemple).





suivant: III.D.2.3 Programmation de I3.
monter: III.D.2 Algorithmes conditionnels de programmation.
précédent: III.D.2.1 Programmation de I1.
Table des matières
Index
Cessenat Olivier
2007-04-21

![]() issues de considérations géométriques. En effet, rappelons que
l'on a défini
issues de considérations géométriques. En effet, rappelons que
l'on a défini
 ,
,
 et
et
 . Si on
remplace
. Si on
remplace ![]() par
par ![]() et
et ![]() par
par ![]() , on sait que
, on sait que




![]() de façon à optimiser la précision du calcul de I2 puis à minimiser le nombre d'opérations à effectuer. Il s'agit d'étudier les précisions
des calculs de I2 par les différentes formules présentées, puis d'obtenir les mêmes précisions sur tous les cas limites afin que la majoration globale de l'erreur sur le calcul de I2 soit aussi faible que possible.
Sous l'hypothèse
de façon à optimiser la précision du calcul de I2 puis à minimiser le nombre d'opérations à effectuer. Il s'agit d'étudier les précisions
des calculs de I2 par les différentes formules présentées, puis d'obtenir les mêmes précisions sur tous les cas limites afin que la majoration globale de l'erreur sur le calcul de I2 soit aussi faible que possible.
Sous l'hypothèse
![]() , les différentes formules de calcul utilisent les trois fonctions suivantes:
, les différentes formules de calcul utilisent les trois fonctions suivantes:
![]() et y=0. On a, puisque
et y=0. On a, puisque ![]() est petit,
est petit,