




suivant: II.9.1.1 Etude du noyau de la matrice
monter: II.9 Analyse de la méthode sur le
précédent: II.9 Analyse de la méthode sur le
Table des matières
Index
II.9.1 Etude de l'erreur d'interpolation.
Cette étude essentielle dans l'analyse de la méthode ne peut reprendre les points expliqués pour le problème de Helmholtz bidimensionnel dans le vide.
Les difficultés majeures proviennent du caractère vectoriel des équations et de la prise en compte des relations de divergence. De plus, les résultats obtenus pour le problème de Helmholtz
ne se généralisent pas simplement au problème de Maxwell tridimensionnel, le choix des fonctions de base n'est plus aussi simple. Nous verrons que choisir des directions de propagation
toutes distinctes ne suffit plus pour contrôler l'erreur d'interpolation.
Nous considérons le problème de Maxwell dans le vide sans terme source, soit le problème sur l'inconnue
(<I>E,<I>H) vérifiant les équations de Maxwell-Faraday et Maxwell-Gauss ci dessous:
|
(II.9.3) |
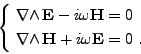 |
Ces relations impliquent dans le vide
|
(II.9.4) |
 |
En posant,
|
(II.9.5) |
 |
nous obtenons le problème équivalent sur
(<I>F,<I>G) devant vérifier les équations de Maxwell (ou conditions de rotationnel)
|
(II.9.6) |
 |
et les relations de Gauss (ou conditions de divergence)
|
(II.9.7) |
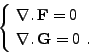 |
Nous supposons que la fonction <I>F solution admet un développement de Taylor uniforme à l'ordre N sur  de telle sorte qu'il existe
de telle sorte qu'il existe
|
(II.9.8) |
 |
coefficients complexes
<I>Fiq1,q2,q3 définissant la fonction polynômiale vectorielle Fa par
et tels que pour tout élément  de
de  il existe une constante C0 strictement positive donnant la majoration
il existe une constante C0 strictement positive donnant la majoration
|
(II.9.9) |
 |
Dans l'hypothèse (II.9.9), h est toujours le paramètre de taille du maillage que l'on suppose régulier, vérifiant les
hypothèses H1, H2 et H3 p. ![[*]](crossref.gif) .
Ceci assure que dans
.
Ceci assure que dans  , on a
, on a
 .
On suppose que les dérivées de <I>F admettent aussi un développement de Taylor uniforme obtenu par dérivation de celui de la fonction <I>F, soit par dérivation
de la fonction polynômiale
<I>Fa.
.
On suppose que les dérivées de <I>F admettent aussi un développement de Taylor uniforme obtenu par dérivation de celui de la fonction <I>F, soit par dérivation
de la fonction polynômiale
<I>Fa.
Nous allons chercher la condition d'existence de p fonctions
<I>Fl vérifiant les équations de Maxwell et les relations de Gauss
|
(II.9.10) |
 |
et admettant un développement de Taylor à l'ordre N sur un élément  de
de  , c'est-à-dire telles que l'on puisse définir les fonctions polynômiales
vectorielles
<I>Fla par les coefficients complexes
<I>Fl,iq1,q2,q3
, c'est-à-dire telles que l'on puisse définir les fonctions polynômiales
vectorielles
<I>Fla par les coefficients complexes
<I>Fl,iq1,q2,q3
|
(II.9.11) |
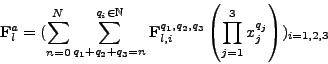 |
tels que
|
(II.9.12) |
 |
et qu'il existe p coefficients complexes bornés  assurant
assurant
|
(II.9.13) |
 |
Si les fonctions
<I>Fl existent, alors on pourra majorer
avec
En conjuguant toutes les relations écrites jusqu'à présent, on aura les mêmes relations avec les coefficients
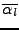 sur les fonctions
<I>Gl par rapport
à la solution <I>G. Alors, en définissant
<I>Ea par
sur les fonctions
<I>Gl par rapport
à la solution <I>G. Alors, en définissant
<I>Ea par
et
<I>Ha par
on obtient que
|
(II.9.14) |
 |
Alors, en posant
on aura, en intégrant sur
 dont la mesure est de l'ordre de h2,
dont la mesure est de l'ordre de h2,
|
(II.9.15) |
 |
puis en sommant sur les
éléments, on a,
soit finalement
|
(II.9.16) |
 |
On a donc
|
(II.9.17) |
 |
La difficulté de notre travail réside maintenant dans le fait de montrer qu'il existe p coefficients  vérifiant (II.9.13), soit
vérifiant (II.9.13), soit
|
(II.9.18) |
 |
pour des fonctions
<I>Fl bien choisies.
Le système (II.9.18) sur les fonctions polynômiales
<I>Fla et
<I>Fa s'écrit de façon équivalente sous la forme d'un
système linéaire sur les coefficients de ces fonctions polynômiales, soit
|
(II.9.19) |
 |
Le système linéaire (II.9.19) écrit sous forme matricielle est équivalent au problème (II.9.20)
dans l'espace vectoriel
 .
.
|
(II.9.20) |
![\begin{displaymath}
\left\{ \null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\str...
...x{ tel que } \cr
& M A = [{{\mathbf F}}] \cr
\crcr}}\, \right. \end{displaymath}](img831.gif) |
Dans (II.9.20)
![$[{{\mathbf F}}] \in {\mathbb{C}}^{\frac{(N+3)(N+2)(N+1)}{2}}$](img832.gif) est un vecteur dont le terme générique est
[<I>F]m=<I>Fiq1,q2,q3.
La matrice M est constituée de p colonnes d'indice l et
est un vecteur dont le terme générique est
[<I>F]m=<I>Fiq1,q2,q3.
La matrice M est constituée de p colonnes d'indice l et
 lignes d'indice m et le terme générique de M est
Mm,l=<I>Fl,iq1,q2,q3.
L'indice de ligne m est une fonction des indices
(i,q1,q2,q3). Nous avons toute liberté de choisir une bijection Q liant
(i,q1,q2,q3) à m de telle sorte que l'on ait
lignes d'indice m et le terme générique de M est
Mm,l=<I>Fl,iq1,q2,q3.
L'indice de ligne m est une fonction des indices
(i,q1,q2,q3). Nous avons toute liberté de choisir une bijection Q liant
(i,q1,q2,q3) à m de telle sorte que l'on ait
|
(II.9.21) |
 |
et
|
(II.9.22) |
![\begin{displaymath}[{{\mathbf F}}]_m = {{\mathbf F}}_{i}^{q_1,q_2,q_3} , \ m=Q(i,q_1,q_2,q_3) \ .
\end{displaymath}](img835.gif) |
Le problème (II.9.20) se ramène à l'étude de l'image et du noyau de M. Nous allons suivre la démarche adoptée pour l'étude du problème
de Helmholtz.
- Montrer que le noyau de M est de dimension supérieure à
 . Ceci s'effectue en analysant les relations linéaires données par les conditions de divergence
et de rotationnel (ou conditions de Gauss et de Maxwell).
. Ceci s'effectue en analysant les relations linéaires données par les conditions de divergence
et de rotationnel (ou conditions de Gauss et de Maxwell).
- Etudier le noyau de M dans le cas simplifié N=1 (il n'y a pas de relation à l'ordre N=0).
- A l'aide d'une construction explicite technique de la fonction Q qui ordonne les indices
(i,q1,q2,q3) dans
 , nous montrons la généralisation pour tout N.
, nous montrons la généralisation pour tout N.
Ce point est conceptuellement aisé à montrer même si la preuve, obligeant à expliciter une loi de construction Q d'un vecteur à partir des indices
(i,q1,q2,q3), est très lourde.
- Montrer qu'il existe un sous espace libre de M de dimension (N+3)(N+1) sous certaines conditions sur le choix des directions de propagation des ondes planes.
- Nous montrons que dans le cas N=0 la matrice M est inversible si et seulement si les p=3 directions de propagation des ondes planes qui construisent l'espace Vh sont distinctes 2 à 2.
- Dans le cas N=1 nous montrons que cette propriété ne se généralise pas.
- La généralisation s'effectue pour tout N sous des hypothèses supplémentaires sur les directions des ondes planes. Plus précisément, nous montrons qu'il existe p=(N+1)(N+3)
ondes planes telles que la matrice M soit inversible.
La démonstration est très longue et très technique.
Sous-sections





suivant: II.9.1.1 Etude du noyau de la matrice
monter: II.9 Analyse de la méthode sur le
précédent: II.9 Analyse de la méthode sur le
Table des matières
Index
Cessenat Olivier
2007-04-21
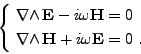


![[*]](crossref.gif) .
Ceci assure que dans
.
Ceci assure que dans 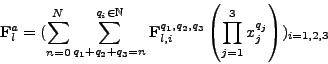


![]() vérifiant (II.9.13), soit
vérifiant (II.9.13), soit
 . Ceci s'effectue en analysant les relations linéaires données par les conditions de divergence
et de rotationnel (ou conditions de Gauss et de Maxwell).
. Ceci s'effectue en analysant les relations linéaires données par les conditions de divergence
et de rotationnel (ou conditions de Gauss et de Maxwell).