III.D.3.1 Vectorisation du calcul de I₁.

Rappelons l'algorithme optimal de programmation de I₁:

• définition ou calcul (portabilité de l'opération) de la précision machine, p_m,
• définition de $\epsilon_1=\sqrt{6p_m}$,
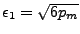• pour tout $\alpha \in {\mathbb{C}}$,
  • si $\vert\alpha\vert \le \epsilon_1$, alors $I_1(\alpha) = L e^{i{{\mathbf k}}\vec{G}}$,
  • sinon $I_1(\alpha) = L e^{i{{\mathbf k}}\vec{G}} \frac{\displaystyle \sin{\alpha}}{\displaystyle \alpha}$.

Cet algorithme, à partir de $\forall \alpha \in {\mathbb{C}}$, peut se transformer en

• calcul de la fonction indicatrice de $\vert\alpha\vert \le \epsilon_1$ notée ${{\mathcal{I}}}_{\left[\vert\alpha\vert\le \epsilon_1 \right]}$ qui vaut 1 si $\vert\alpha\vert \le \epsilon_1$, qui vaut 0 sinon,
• calcul direct de I₁ par la formule analytique
  

  $$I_1(\alpha)=L e^{i{{\mathbf k}}\vec{G}} e^{i\alpha} \left( (... ...al{I}}}_{\left[\vert\alpha\vert\le \epsilon_1 \right]} \right)$$ (III.D.21)

  
  

sans rien changer à la précision du calcul, de l'ordre de p_m. Sur calculateur Cray, nous proposons de calculer la fonction indicatrice à l'aide de la formule

$${{\mathcal{I}}}_{\left[\vert\alpha\vert\le \epsilon_1 \right]}=\max(0,nint(sign(1.,\epsilon_1-\vert\alpha\vert)))$$ (III.D.22)

qui n'utilise que des fonctions intrinsèques au calculateur, fonctions dont la vectorisation est ``totale''.

Remarque 53   On peut aussi calculer ${{\mathcal{I}}}_{\left[\vert\alpha\vert\le \epsilon_1 \right]}$ par

$$% {{\mathcal{I}}}_{\left[\vert\alpha\vert\le \epsilon_1 \right]}=nint(0.5+sign(0.5,\vert\alpha\vert-\epsilon_1))$$ (III.D.23)

et aussi la fonction $I_1(\alpha)$ par

$$% I_1(\alpha)= L e^{i{{\mathbf k}}\vec{G}} e^{i\alpha} \left(... ...}}}_{\left[\vert\alpha\vert\le \epsilon_1 \right]} \right) \ .$$ (III.D.24)