




suivant: III.B Mise en uvre informatique de l'espace
monter: 3 Annexes
précédent: 3 Annexes
Table des matières
Index
III.A Mise en  uvre informatique de l'espace Vh choisi pour Helmholtz.
uvre informatique de l'espace Vh choisi pour Helmholtz.
Nous calculons analytiquement les termes des matrices et du second membre de la formulation discrète (I.1.27) du problème modèle de Helmholtz bidimensionnel sans
coefficient. L'espace de discrétisation est l'espace Vh construit à l'aide des ondes planes section I.2.2.1. Nous donnons d'abord les notations nécessaires à
cette section.
- i)
- Notations relatives à la géométrie (sommets, arêtes, normales, longueurs).
- Soient
(x1k,x2k,x3k) les positions des trois sommets du triangle
 .
.
- Soient
(x1kj,x2kj) les extrémités de l'arête
 commune aux éléments
commune aux éléments  et
et  .
.
- Soient
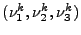 les trois normales sortantes du
triangle
les trois normales sortantes du
triangle  , respectivement des arêtes
(x1k,x2k), (x2k,x3k) et (x3k,x1k).
, respectivement des arêtes
(x1k,x2k), (x2k,x3k) et (x3k,x1k).
- Soit
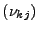 la normale sortante du triangle
la normale sortante du triangle  vers le triangle
vers le triangle  . C'est donc aussi la normale à l'arête
(x1kj,x2kj).
. C'est donc aussi la normale à l'arête
(x1kj,x2kj).
- Soient
(L1k,L2k,L3k) les longueurs des trois arêtes du triangle
 : |x1k-x2k|, |x2k-x3k|, |x3k-x1k|.
: |x1k-x2k|, |x2k-x3k|, |x3k-x1k|.
- Soit Lkj la longueur de l'arête
 :
|x1kj-x2kj|.
:
|x1kj-x2kj|.
- ii)
- Notations relatives aux termes exponentiels des fonctions de base.
- Pour n=1 à 3,
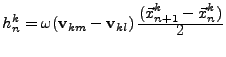 avec
avec
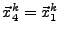 .
.
- Pour n=1 à 3,
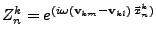 .
.
- Soit
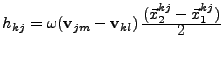 .
.
- Soit
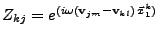 .
.
Les matrices D (I.2.18) et C (I.2.19 et I.2.20) et le second membre
b (I.2.21) donnés section I.2.1.4 sont calculés à l'aide des ondes planes définissant l'espace de discrétisation Vh.
- i)
- Le calcul de D (I.2.18) pour des ondes planes fait apparaître un terme constant à multiplier par l'intégrale d'une onde plane sur un segment.
A l'aide de l'annexe III.D.1.1 qui donne l'intégrale sur un segment de la fonction
ei<I>k<I>X, on calcule facilement que les termes non nuls de D,
notés Dkl,m, sont explicités par
|
(III.A.1) |
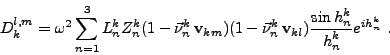 |
Le terme Dkl,m est la somme des contributions des arêtes de l'élément  pour les fonctions de base de directions
vkm et
vkl.
pour les fonctions de base de directions
vkm et
vkl.
- ii)
- La matrice C, constituée de termes de couplage entre
deux éléments voisins (I.2.19) et de termes diagonaux de couplage au bord du domaine (I.2.20), est calculée de la même
façon que D. On obtient donc après calculs (qui utilisent toujours l'intégrale sur un segment de la fonction
ei<I>k<I>X de l'annexe III.D.1.1)
les deux formules de calcul des termes non nuls de C (III.A.2) et (III.A.3) ci-dessous.
- Dans le cas où
 est voisin de
est voisin de  , la contribution Ck,jl,m de l'interface
, la contribution Ck,jl,m de l'interface  pour les fonctions de base de directions
vjm et
vkl
est donnée par
pour les fonctions de base de directions
vjm et
vkl
est donnée par
|
(III.A.2) |
 |
- Dans le cas où
 est non vide, la contribution Ck,kl,m du bord
est non vide, la contribution Ck,kl,m du bord  pour les fonctions de base sur
pour les fonctions de base sur  de directions
vkm et
vkl
est donnée par
de directions
vkm et
vkl
est donnée par
|
(III.A.3) |
![\begin{displaymath}
C_{k,k}^{l,m} = \sum_{n / [x_n^k,x_{n+1}^k] \in \Gamma_k}{{{...
...h_n^k } \frac{\displaystyle \sin{h_n^k}}{\displaystyle h_n^k}}
\end{displaymath}](img1146.gif) |
où l'on utilise l'hypothèse
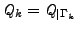 constant sur
constant sur  .
.
- iii)
- Le second membre, donné par l'équation (I.2.21), est calculé pour des fonctions de base issues d'ondes planes par
|
(III.A.4) |
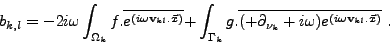 |
Nous explicitons le calcul analytique de (III.A.4) dans les cas suivants de valeurs des fonctions f et g.
- La contribution d'un terme source localisé en un point x0 de
 , soit pour
, soit pour
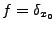 , est donnée par
, est donnée par
|
(III.A.5) |
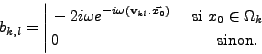 |
- La contribution d'une source surfacique sur un bord
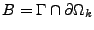 correspondant à l'excitation par une onde plane incidente de direction
v0, modélisée
par
correspondant à l'excitation par une onde plane incidente de direction
v0, modélisée
par
où l'on suppose
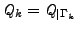 constant, est
constant, est
|
(III.A.6) |
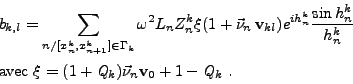 |
- On calcule la contribution d'une source volumique
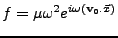 . Sur un triangle de surface S et de barycentre
. Sur un triangle de surface S et de barycentre  , le calcul de l'intégrale
de l'onde plane
ei<I>k<I>X est effectué annexe III.D.1.2. Alors, pour
, le calcul de l'intégrale
de l'onde plane
ei<I>k<I>X est effectué annexe III.D.1.2. Alors, pour
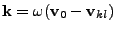 , la contribution de la source
volumique f est, pour un triangle
, la contribution de la source
volumique f est, pour un triangle 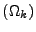 ,
,
|
(III.A.7) |
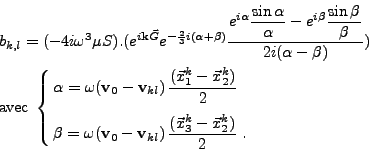 |
La mise en  uvre informatique du calcul des termes explicités ci-dessus n'est pas directe. En effet, les intégrations des ondes planes sur un segment ou sur un triangle donnent des fonctions dont
le domaine de définition pose problème.
uvre informatique du calcul des termes explicités ci-dessus n'est pas directe. En effet, les intégrations des ondes planes sur un segment ou sur un triangle donnent des fonctions dont
le domaine de définition pose problème.
- Les termes matriciels D et C ne sont pas définis pour
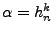 ou
ou 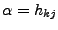 nuls. En effet, la fonction
nuls. En effet, la fonction  , intégrale sur un segment [x1,x2] de
ei<I>k<I>X,
vaut
, intégrale sur un segment [x1,x2] de
ei<I>k<I>X,
vaut
où  est la position du barycentre du segment et L sa longueur,
est la position du barycentre du segment et L sa longueur,  est donné par
est donné par
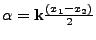 . Cette
fonction, qui permet de calculer les termes matriciels, est définie sur
. Cette
fonction, qui permet de calculer les termes matriciels, est définie sur
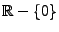 . Elle se prolonge mathématiquement par continuité en 0, mais cette notion est ignorée par les calculateurs.
Nous expliquons annexe III.D.2.1 comment calculer la fonction
. Elle se prolonge mathématiquement par continuité en 0, mais cette notion est ignorée par les calculateurs.
Nous expliquons annexe III.D.2.1 comment calculer la fonction  sur
sur  ou
ou  sur tout calculateur de façon à obtenir la meilleure précision possible.
Le lecteur intéressé par les problèmes d'optimisation sur ``super-calculateurs'' consultera l'annexe III.D.3.1 pour l'implémentation sur machine à architecture
vectorielle.
sur tout calculateur de façon à obtenir la meilleure précision possible.
Le lecteur intéressé par les problèmes d'optimisation sur ``super-calculateurs'' consultera l'annexe III.D.3.1 pour l'implémentation sur machine à architecture
vectorielle.
- Le calcul du second membre dans le cas d'une source volumique de la forme
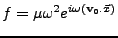 n'est pas défini sur les droites
n'est pas défini sur les droites  ,
,  et
et  dans l'équation (III.A.7). Comme pour l'intégrale sur un segment
dans l'équation (III.A.7). Comme pour l'intégrale sur un segment  , nous expliquons, annexe III.D.2.2, comment calculer par ordinateur
la fonction intégrale sur un triangle [x1,x2,x3] de surface S de
ei<I>k<I>X, soit, pour
, nous expliquons, annexe III.D.2.2, comment calculer par ordinateur
la fonction intégrale sur un triangle [x1,x2,x3] de surface S de
ei<I>k<I>X, soit, pour  la position du barycentre du triangle
et
la position du barycentre du triangle
et
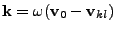 ,
,
et comment optimiser le calcul sur machine vectorielle annexe III.D.3.2.
Le lecteur trouvera comment nous avons optimisé le problème suivant:
- garder une excellente précision de calcul,
- effectuer le calcul le plus rapidement possible.





suivant: III.B Mise en uvre informatique de l'espace
monter: 3 Annexes
précédent: 3 Annexes
Table des matières
Index
Cessenat Olivier
2007-04-21
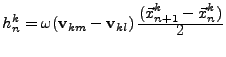 avec
avec
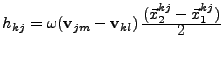 .
.
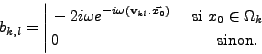
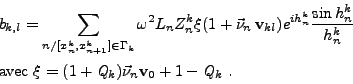
![]() uvre informatique du calcul des termes explicités ci-dessus n'est pas directe. En effet, les intégrations des ondes planes sur un segment ou sur un triangle donnent des fonctions dont
le domaine de définition pose problème.
uvre informatique du calcul des termes explicités ci-dessus n'est pas directe. En effet, les intégrations des ondes planes sur un segment ou sur un triangle donnent des fonctions dont
le domaine de définition pose problème.
