




suivant: III.B.1.2 Forme des matrices.
monter: III.B.1 Construction du système linéaire.
précédent: III.B.1 Construction du système linéaire.
Table des matières
Index
III.B.1.1 Introduction, notations.
Nous considérons les contributions d'une interface  ou d'une face de bord
ou d'une face de bord
 sans effectuer l'éventuelle sommation sur toutes les faces
sans effectuer l'éventuelle sommation sur toutes les faces  concernées
(par exemple dans le calcul des termes de la matrice D ou du second membre). Nous laissons au lecteur le soin de calculer les contributions d'une face quadrangulaire et d'effectuer les sommations
adéquates. Nous considérons les quantités qui dépendent de la géométrie de l'interface
concernées
(par exemple dans le calcul des termes de la matrice D ou du second membre). Nous laissons au lecteur le soin de calculer les contributions d'une face quadrangulaire et d'effectuer les sommations
adéquates. Nous considérons les quantités qui dépendent de la géométrie de l'interface  , des fonctions de base et du milieu présent de part et d'autre de l'interface.
, des fonctions de base et du milieu présent de part et d'autre de l'interface.
- Les trois sommets de l'interface
 sont notés
sont notés
|
(III.B.1) |
 |
Pour faciliter un jeu d'écriture, on utilisera
<I>Xk,j4 désignant
<I>Xk,j1, et ainsi de suite.
- Nous notons Sk,j la surface de la face plane
 . Ce terme est calculé par
. Ce terme est calculé par
|
(III.B.2) |
 |
- Pour
 , indices des directions de propagation dans
, indices des directions de propagation dans  ou
ou  , on note
, on note
|
(III.B.3) |
 |
- Sur les trois arêtes définissant
 et pour les directions de propagation définissant
vk,jl,m (III.B.3), on pose
et pour les directions de propagation définissant
vk,jl,m (III.B.3), on pose
|
(III.B.4) |
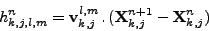 |
et
|
(III.B.5) |
 |
- Nous notons fk,jl,m le terme intégral sur
 de l'onde plane définie par son vecteur d'onde
2vk,jl,m:
de l'onde plane définie par son vecteur d'onde
2vk,jl,m:
|
(III.B.6) |
 |
Nous noterons abusivement fk,kl,m l'intégrale sur  (et non sur
(et non sur  )
)
|
(III.B.7) |
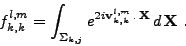 |
Cette intégrale dépend de la géométrie de  mais ne dépend que des fonctions de base de
mais ne dépend que des fonctions de base de  : en toute rigueur, il faudrait introduire un troisième
indice et noter
fk,k,jl,m.
: en toute rigueur, il faudrait introduire un troisième
indice et noter
fk,k,jl,m.
Nous calculons annexe III.D.1.2 l'intégrale de
ei<I>k<I>X sur une face plane triangulaire. D'après la relation (III.D.5)
pour
<I>k= 2ivk,jl,m , on calcule analytiquement fk,jl,m par
|
(III.B.8) |
 |
indépendamment de n, l'indice des sommets
<I>Xk,jn de  . A l'aide du barycentre
. A l'aide du barycentre  de l'interface
de l'interface  , on a aussi
, on a aussi
|
(III.B.9) |
 |
ou, à l'aide de
vk,jl,m (III.B.3),
|
(III.B.10) |
 |
L'implémentation informatique de cette formule et son implémentation sur une machine à architecture vectorielle sont présentées dans les annexes III.D.2.2
et III.D.3.2.
Les formules donnant l'intégrale fk,kl,m s'obtiennent des formules ci-dessus en remplaçant j par k partout où apparaissent les fonctions de base, mais pas dans les
termes intrinsèques à la géométrie.
Enfin, rappelons quelques définitions ou notations qui servent dans ce chapitre.
Nous utiliserons aussi, pour  , la notation
, la notation
|
(III.B.16) |
 |
Remarque 48 D'après (
III.B.13), on a
d'où
Si

et

sont réels sur

alors
|
(III.B.17) |
 |





suivant: III.B.1.2 Forme des matrices.
monter: III.B.1 Construction du système linéaire.
précédent: III.B.1 Construction du système linéaire.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() ou d'une face de bord
ou d'une face de bord
![]() sans effectuer l'éventuelle sommation sur toutes les faces
sans effectuer l'éventuelle sommation sur toutes les faces ![]() concernées
(par exemple dans le calcul des termes de la matrice D ou du second membre). Nous laissons au lecteur le soin de calculer les contributions d'une face quadrangulaire et d'effectuer les sommations
adéquates. Nous considérons les quantités qui dépendent de la géométrie de l'interface
concernées
(par exemple dans le calcul des termes de la matrice D ou du second membre). Nous laissons au lecteur le soin de calculer les contributions d'une face quadrangulaire et d'effectuer les sommations
adéquates. Nous considérons les quantités qui dépendent de la géométrie de l'interface ![]() , des fonctions de base et du milieu présent de part et d'autre de l'interface.
, des fonctions de base et du milieu présent de part et d'autre de l'interface.


![]() , la notation
, la notation