




suivant: II.10.3.2 Etude exhaustive sur un cas de
monter: II.10.3 Maillages tétraédriques ou hexaédriques.
précédent: II.10.3 Maillages tétraédriques ou hexaédriques.
Table des matières
Index
Nous avons effectué des simulations pour trois très basses fréquences par rapport au paramètre h de raffinement du maillage. Les fréquences de calculs sont 105, 95 ou 85 MHz, les longueurs
d'onde sont donc respectivement de 2.857, 3.158 et 3.529 mètres.
La figure II.10.27 représente l'évolution de la précision de la norme L2 relative
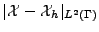 en fonction du nombre d'itérations effectuées pour
les trois maillages. Notons que la figure II.10.27 a) avec 11 directions de propagation aléatoires entre les éléments est issue d'un calcul effectué en une seule fois, de
105 MHz à 85 MHz par pas de -10 MHz, ce qui explique que le nombre d'itérations effectuées est plus grand pour la première fréquence. La figure II.10.27 b) ne
concerne que la plus basse fréquence de 85 MHz et est obtenue pour 13 directions de propagation aléatoires entre les éléments.
en fonction du nombre d'itérations effectuées pour
les trois maillages. Notons que la figure II.10.27 a) avec 11 directions de propagation aléatoires entre les éléments est issue d'un calcul effectué en une seule fois, de
105 MHz à 85 MHz par pas de -10 MHz, ce qui explique que le nombre d'itérations effectuées est plus grand pour la première fréquence. La figure II.10.27 b) ne
concerne que la plus basse fréquence de 85 MHz et est obtenue pour 13 directions de propagation aléatoires entre les éléments.
Figure II.10.27:
Nombre d'itérations et précision selon les types de maillages, cas limite sur-discrétisé.
![\includegraphics[width=0.47\columnwidth,height=0.44\columnwidth]{evolitertypea11RbalFre.ps}](img1126.gif) |
![\includegraphics[width=0.47\columnwidth,height=0.44\columnwidth]{evolitertypea13RbalFre.ps}](img1127.gif) |
| a) Balayage fréquentiel pour 11 directions. |
b) Calcul à 85 MHz avec 13 directions. |
|
Les rapports entre la longueur d'onde et le raffinement du maillage sont données dans les tableaux II.10.14 et II.10.15 pour respectivement 105
et 85 MHz pour les trois maillages.
Tableau II.10.14:
Maillages tétraédriques ou hexaédriques, simulation à 105 MHz.
| Quantité |
Maillage M1 |
Maillage M2 |
Maillage M3 |
 |
37 |
38 |
39 |
| Conditionnement |
1.1E11 |
3.2E10 |
8.2E10 |
 |
1.4E-5 |
1.7E-5 |
4.2E-5 |
Nous donnons quelques informations pour la simulation avec 11 directions de propagation par élément (choisies aléatoirement entre les éléments) sur le conditionnement maximal des sous matrices
Dk (cf section II.8.1.2) de D et la qualité de l'inversion de la matrice globale D (chapitre II.8, problème (II.8.2)), comme nous l'avions déjà indiqué dans la section II.10.1.2.2, en norme  sur l'erreur maximale des
coefficients de D-1D par rapport à la matrice identité I.
sur l'erreur maximale des
coefficients de D-1D par rapport à la matrice identité I.
Tableau II.10.15:
Maillages tétraédriques ou hexaédriques, simulation à 85 MHz.
| Quantité |
Maillage M1 |
Maillage M2 |
Maillage M3 |
 |
46 |
47 |
48 |
| Conditionnement |
3,2E10 |
9,0E9 |
2,3E10 |
 |
3,6E-6 |
5,8E-6 |
8,6E-6 |
Nous constatons sur ce cas précis les points suivants.
- Le nombre d'itérations nécessaires pour les trois fréquences 105, 95 et 85 MHz est inférieur pour le maillage hexaédrique que pour les deux autres maillages tétraédriques.
Le coût supplémentaire en temps de calcul induit par le maillage en hexaèdre est donc compensé par la plus grande rapidité de résolution du système linéaire.
- La précision finale est meilleure avec le maillage en hexaèdre. Le coût supplémentaire en place mémoire induit par le maillage en hexaèdre peut donc être compensé par l'utilisation
d'un maillage moins fin, donc moins compliqué à construire.
- Le maillage en hexaèdre est plus robuste par rapport au conditionnement des matrices hermitiennes de produit scalaire Dk, trop élevé comme on le constate dans le tableau II.10.14. Cela permet d'obtenir des résultats plus précis en sur-discrétisant.





suivant: II.10.3.2 Etude exhaustive sur un cas de
monter: II.10.3 Maillages tétraédriques ou hexaédriques.
précédent: II.10.3 Maillages tétraédriques ou hexaédriques.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() en fonction du nombre d'itérations effectuées pour
les trois maillages. Notons que la figure II.10.27 a) avec 11 directions de propagation aléatoires entre les éléments est issue d'un calcul effectué en une seule fois, de
105 MHz à 85 MHz par pas de -10 MHz, ce qui explique que le nombre d'itérations effectuées est plus grand pour la première fréquence. La figure II.10.27 b) ne
concerne que la plus basse fréquence de 85 MHz et est obtenue pour 13 directions de propagation aléatoires entre les éléments.
en fonction du nombre d'itérations effectuées pour
les trois maillages. Notons que la figure II.10.27 a) avec 11 directions de propagation aléatoires entre les éléments est issue d'un calcul effectué en une seule fois, de
105 MHz à 85 MHz par pas de -10 MHz, ce qui explique que le nombre d'itérations effectuées est plus grand pour la première fréquence. La figure II.10.27 b) ne
concerne que la plus basse fréquence de 85 MHz et est obtenue pour 13 directions de propagation aléatoires entre les éléments.
![]() sur l'erreur maximale des
coefficients de D-1D par rapport à la matrice identité I.
sur l'erreur maximale des
coefficients de D-1D par rapport à la matrice identité I.