I.5.2.3 Choix de l'espace d'approximation et résolution du système linéaire.

L'introduction des coefficients dans le problème de Helmholtz bidimensionnel nous amène à définir des solutions de $-\mathop{\nabla .}\nolimits [ \mu^{*}\mathop{{\mathbf {\nabla }}}\nolimits e_k] -\omega^2 \overline{\rho} e_k = 0$ sous la forme d'ondes planes:

$$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...rho}{\displaystyle \mu }} \vec{ x})} \ . \cr \crcr}}\, \right.$$

En effet,

$$\mathop{{\mathbf {\nabla }}}\nolimits e_k = i\omega { \vec{ ... ...{\frac{\displaystyle \rho}{\displaystyle \mu }} \vec{ x})} \ ,$$

d'où

$$\mu^{*}\mathop{{\mathbf {\nabla }}}\nolimits e_k = \sqrt{\mu... ...sqrt{\frac{\displaystyle \rho}{\displaystyle \mu }} \vec{ x})}$$

et finalement

$$\mathop{\nabla .}\nolimits [ \mu^{*}\mathop{{\mathbf {\nabla... ...{\frac{\displaystyle \rho}{\displaystyle \mu }} \vec{ x})} \ .$$

Remarque 30   Nous sommes toujours libres de choisir les directions de propagation v_k,l des ondes planes comme en I.2.29 équiréparties dans le plan. De même, il est possible d'utiliser des informations d'études asymptotiques du comportement de la solution et d'introduire les ondes de pression et de cisaillement adéquates.

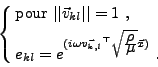
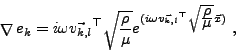
Le système (I.5.36) est résolu comme dans le cas sans coefficient. L'inversibilité de la matrice D est assurée pour des ondes planes si et seulement si les vecteurs d'onde sont tous distincts $\forall k, (\forall (i,j), \vec{v}_{ki} \ne \vec{v}_{kj})$ puisque la matrice $\sqrt{\frac{\displaystyle \rho}{\displaystyle \mu }}$ est définie positive.