




suivant: I.5.1.2 Nouvelle formulation variationnelle.
monter: I.5.1 Présentation du problème et formulation.
précédent: I.5.1 Présentation du problème et formulation.
Table des matières
Index
Nous étudions la généralisation du problème modèle (I.0.1) au cas de la propagation acoustique plan dans un milieu
borné  , de frontière
, de frontière  lipschitzienne, constitué de matériaux aux caractéristiques constantes par morceaux qui définissent le
tenseur bidimensionnel
lipschitzienne, constitué de matériaux aux caractéristiques constantes par morceaux qui définissent le
tenseur bidimensionnel  et la fonction scalaire
et la fonction scalaire 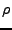 . On modélise ce phénomène par
. On modélise ce phénomène par
|
(I.5.1) |
 |
où  est une fonction essentiellement bornée et
est une fonction essentiellement bornée et  un opérateur réel de norme strictement inférieure à 1.
Les hypothèses physiques sur les fonctions
un opérateur réel de norme strictement inférieure à 1.
Les hypothèses physiques sur les fonctions  ,
, 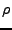 et
et  sont qu'elles sont supérieurement et inférieurement essentiellement bornées, soit,
(au sens matriciel pour
sont qu'elles sont supérieurement et inférieurement essentiellement bornées, soit,
(au sens matriciel pour  ),
),
|
(I.5.2) |
 |
D'autre part, on suppose que le milieu est dissipatif, soit
|
(I.5.3) |
 |
Remarquons que pour  ,
,  et
et  la matrice identité du plan, le problème (I.5.1) est le problème de Helmholtz
sans coefficient traité dans cette première partie. En effet, l'opérateur
la matrice identité du plan, le problème (I.5.1) est le problème de Helmholtz
sans coefficient traité dans cette première partie. En effet, l'opérateur
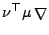 vérifie alors
vérifie alors
La formulation variationnelle classique est (en posant
 avec
avec
 )
)
|
(I.5.4) |
 |
L'hypothèse
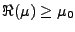 définie positive signifie que la forme
définie positive signifie que la forme
|
(I.5.5) |
![\begin{displaymath}%
(u,v) \in [H^{1}(\Omega)]^2 \mapsto \int_{\Omega} { \mathop...
...bf {\nabla }}}\nolimits { \overline{ v}} + u \, \overline{ v}
\end{displaymath}](img429.gif) |
est coercive sur  .
On montre ensuite que l'opérateur
.
On montre ensuite que l'opérateur
|
(I.5.6) |
![\begin{displaymath}%
(u,v) \in [H^{1}(\Omega)]^2 \mapsto -(1+\omega^2) \int_{\Om...
...overline{ v} } +i\omega\int_{\Gamma} \zeta u \, \overline{ v}
\end{displaymath}](img431.gif) |
est une perturbation compacte de l'opérateur coercif par l'injection compacte de 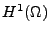 dans
dans  pour
pour  borné ([23]) et par l'injection continue
de
borné ([23]) et par l'injection continue
de
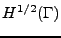 dans
dans  .
Cela nous place dans le cadre de l'alternative de Fredholm.
de conclure à l'existence et l'unicité du problème continu.
.
Cela nous place dans le cadre de l'alternative de Fredholm.
de conclure à l'existence et l'unicité du problème continu.
On utilise alors le fait que
 et
et
 et
et
 : ceci permet de montrer l'unicité par le théorème de prolongement
d'Holmgren.
: ceci permet de montrer l'unicité par le théorème de prolongement
d'Holmgren.
Par la suite, nous supposerons que  est réel.
est réel.





suivant: I.5.1.2 Nouvelle formulation variationnelle.
monter: I.5.1 Présentation du problème et formulation.
précédent: I.5.1 Présentation du problème et formulation.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() , de frontière
, de frontière ![]() lipschitzienne, constitué de matériaux aux caractéristiques constantes par morceaux qui définissent le
tenseur bidimensionnel
lipschitzienne, constitué de matériaux aux caractéristiques constantes par morceaux qui définissent le
tenseur bidimensionnel ![]() et la fonction scalaire
et la fonction scalaire ![]() . On modélise ce phénomène par
. On modélise ce phénomène par


![]() ,
, ![]() et
et ![]() la matrice identité du plan, le problème (I.5.1) est le problème de Helmholtz
sans coefficient traité dans cette première partie. En effet, l'opérateur
la matrice identité du plan, le problème (I.5.1) est le problème de Helmholtz
sans coefficient traité dans cette première partie. En effet, l'opérateur
![]() vérifie alors
vérifie alors
![]() avec
avec
![]() )
)

![]() et
et
![]() et
et
![]() : ceci permet de montrer l'unicité par le théorème de prolongement
d'Holmgren.
: ceci permet de montrer l'unicité par le théorème de prolongement
d'Holmgren.
![]() est réel.
est réel.