




suivant: III.B.2.1 Reconstruction des champs électrique et magnétique
monter: III.B Mise en uvre informatique de l'espace
précédent: III.B.1.4 Assemblage du second membre, cas particuliers.
Table des matières
Index
III.B.2 Reconstruction des champs électrique et magnétique.
La solution
 du problème variationnel (II.7.84) est approchée par une fonction
du problème variationnel (II.7.84) est approchée par une fonction
 à l'aide des coefficients complexes
à l'aide des coefficients complexes
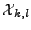 solutions
du système linéaire (II.8.12) et des fonctions de base
solutions
du système linéaire (II.8.12) et des fonctions de base
 définies en (II.8.29):
définies en (II.8.29):
Montrons comment nous pouvons reconstruire les fonctions approchées
<I>Eh et
<I>Hh des solutions <I>E et <I>H du problème initial de Maxwell (1 p. ![[*]](crossref.gif) ) à
l'aide des fonctions
(<I>E<I>Fk,l,<I>H<I>Fk,l) ((II.8.22) et (II.8.25)) pour
) à
l'aide des fonctions
(<I>E<I>Fk,l,<I>H<I>Fk,l) ((II.8.22) et (II.8.25)) pour  et
(<I>E<I>Gk,l-p,<I>H<I>Gk,l-p) ((II.8.23) et (II.8.26)) pour
et
(<I>E<I>Gk,l-p,<I>H<I>Gk,l-p) ((II.8.23) et (II.8.26)) pour
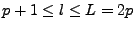 . Cette section s'attache à construire
ces solutions approchées dans trois situations:
. Cette section s'attache à construire
ces solutions approchées dans trois situations:
- i)
- reconstruction dans tout le domaine
 ,
,
- ii)
- reconstruction des traces tangentielles des champs sur le maillage,
- iii)
- reconstruction des traces sur le maillage.
Sous-sections





suivant: III.B.2.1 Reconstruction des champs électrique et magnétique
monter: III.B Mise en uvre informatique de l'espace
précédent: III.B.1.4 Assemblage du second membre, cas particuliers.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() du problème variationnel (II.7.84) est approchée par une fonction
du problème variationnel (II.7.84) est approchée par une fonction
![]() à l'aide des coefficients complexes
à l'aide des coefficients complexes
![]() solutions
du système linéaire (II.8.12) et des fonctions de base
solutions
du système linéaire (II.8.12) et des fonctions de base
![]() définies en (II.8.29):
définies en (II.8.29):
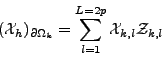
![[*]](crossref.gif) ) à
l'aide des fonctions
(<I>E<I>Fk,l,<I>H<I>Fk,l) ((II.8.22) et (II.8.25)) pour
) à
l'aide des fonctions
(<I>E<I>Fk,l,<I>H<I>Fk,l) ((II.8.22) et (II.8.25)) pour