




suivant: III.D.3.3 Vectorisation du calcul de I3.
monter: III.D.3 Recettes d'implémentation sur machine vectorielle.
précédent: III.D.3.1 Vectorisation du calcul de I1.
Table des matières
Index
III.D.3.2 Vectorisation du calcul de I2.
La vectorisation devient compliquée, mais est encore abordable.
Pour cela, il faut calculer tous les termes définis section III.D.2.2 de façon
à ce qu'ils soient définis sur
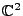 .
.
On définit toujours les fonctions caractéristiques par rapport aux quantités  et
et 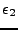 .
.
|
(III.D.25) |
![\begin{displaymath}
{{\mathcal{I}}}_{\left[\vert\alpha\vert\ge \epsilon \right]}=\max(0,nint(sign(1.,\vert\alpha\vert-\epsilon)))
\end{displaymath}](img1482.gif) |
On utilise aussi la fonction  définie et calculée sur
définie et calculée sur  par
par
|
(III.D.26) |
![\begin{displaymath}
f(\alpha)=e^{i\alpha} \left( {{\mathcal{I}}}_{\left[\vert\al...
...}}}_{\left[\vert\alpha\vert\ge \epsilon_1 \right]} \right) \ .
\end{displaymath}](img1483.gif) |
On calcule alors T1 et T2 ainsi que le développement limité
 (III.D.12),
(III.D.12),
|
(III.D.27) |
![\begin{displaymath}%
\null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\strut\hfil...
...}_{\left[\vert\beta\vert\ge \epsilon_2 \right]}} \cr
\crcr}}\,
\end{displaymath}](img1485.gif) |
et l'on a finalement
|
(III.D.28) |
![\begin{displaymath}
\null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\strut\hfil$...
...left[\vert\beta\vert\ge \epsilon_2 \right]}) \ . \cr
\crcr}}\,
\end{displaymath}](img1486.gif) |





suivant: III.D.3.3 Vectorisation du calcul de I3.
monter: III.D.3 Recettes d'implémentation sur machine vectorielle.
précédent: III.D.3.1 Vectorisation du calcul de I1.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() .
.
![]() et
et ![]() .
.
![\begin{displaymath}%
\null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\strut\hfil...
...}_{\left[\vert\beta\vert\ge \epsilon_2 \right]}} \cr
\crcr}}\,
\end{displaymath}](img1485.gif)