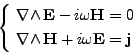suivant: II.7.1.2 Cadre mathématique usuel et résultats d'existence
monter: II.7.1 Rappels sur le problème de Maxwell.
précédent: II.7.1 Rappels sur le problème de Maxwell.
Table des matières
Index
Nous traitons du problème de Maxwell stationnaire dans un domaine tridimensionnel  décrit par la permittivité
décrit par la permittivité  et la perméabilité
et la perméabilité  , fonctions de
la fréquence f (ou de la pulsation
, fonctions de
la fréquence f (ou de la pulsation
 ) et de la position notée <I>X. Les ondes électromagnétiques décrites par les champs électrique
<I>E et magnétique <I>H sont éventuellement perturbées par des termes sources volumiques d'énergie finie, la densité de courant électrique <I>j et
la densité de charge magnétique <I>m. Nous formulons en outre les hypothèses suivantes:
) et de la position notée <I>X. Les ondes électromagnétiques décrites par les champs électrique
<I>E et magnétique <I>H sont éventuellement perturbées par des termes sources volumiques d'énergie finie, la densité de courant électrique <I>j et
la densité de charge magnétique <I>m. Nous formulons en outre les hypothèses suivantes:
- le milieu de propagation est dissipatif, ce qui, dans la convention qui définit la transformée de Fourier d'une fonction f par
 ,
s'exprime par
,
s'exprime par
|
(II.7.1) |
 |
- les fonctions
 et
et  sont inférieurement bornées: il existe
sont inférieurement bornées: il existe
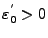 et
et  tels que
tels que
|
(II.7.2) |
 |
Dans le vide, la permittivité
 et la perméabilité
et la perméabilité  définissent la célérité ou vitesse de propagation c des ondes électromagnétiques par
définissent la célérité ou vitesse de propagation c des ondes électromagnétiques par
|
(II.7.3) |
 |
Nous pouvons donc définir la permittivité et la perméabilité du milieu relativement au vide,
 et
et  , par
, par
|
(II.7.4) |
 |
Par la suite, nous considérerons toujours les permittivité et perméabilité relatives que nous noterons dorénavant  et
et  puisqu'il n'y aura pas risque de confusion.
Les caractéristiques du vide seront alors naturellement
puisqu'il n'y aura pas risque de confusion.
Les caractéristiques du vide seront alors naturellement
 et
et  .
.
Sous ces hypothèses, l'onde électromagnétique
(<I>E,<I>H) vérifie les équations de Maxwell harmoniques à la pulsation  dans le domaine
dans le domaine 
|
(II.7.5) |
 |
où les termes sources volumiques <I>m et <I>j vérifient
Notons que physiquement, la quantité de charge magnétique <I>m n'existe pas mais nous la gardons pour la symétrie des équations.
Nous pouvons définir les quantités suivantes qui sont intrinsèques au milieu de propagation:
- le nombre d'onde k,
|
(II.7.6) |
 |
- la longueur d'onde
 ,
,
|
(II.7.7) |
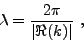 |
- l'indice du milieu n,
|
(II.7.8) |
 |
- l'impédance relative du milieu Z (ou impédance intrinsèque [55]), de partie réelle positive,
|
(II.7.9) |
 |
Rappelons que dans un domaine infini le champ électromagnétique
(<I>E,<I>H) doit vérifier la condition de radiation de Silver-Müller, condition qui s'écrit pour une
position  à l'infini (dans un domaine complémentaire d'un borné) dans le vide où
à l'infini (dans un domaine complémentaire d'un borné) dans le vide où
 (d'après II.7.4):
(d'après II.7.4):
|
(II.7.10) |
 |
Le champ à l'infini de la solution du problème (II.7.5) est donné, au premier ordre en r, par
où a et b ne dépendent pas de r. On a donc, pour
 ,
,
Cette condition, écrite sur une sphère de rayon r en un point où le vecteur  est la normale
est la normale  , donne de façon équivalente
, donne de façon équivalente
Notons que cette condition aux limites n'est pas très performante pour approcher le problème infini en domaine borné. Nous ne discuterons pas ce point qui ne fait pas l'objet de notre exposé.
En domaine borné, nous pouvons écrire cette condition aux limites sur une frontière sphérique éloignée du centre du domaine (cf figure II.7.1)
de façon à obtenir une condition aux limites absorbante d'ordre le plus faible ([8] ou [30]). Nous généralisons cette condition à tout domaine borné, assez
régulier pour pouvoir définir la normale sortante  sur son bord extérieur
sur son bord extérieur
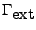 (que l'on suppose placé dans le vide, comme c'est le cas
figure II.7.1), en présence d'un terme de courant de surface g. On obtient la condition aux limites
(que l'on suppose placé dans le vide, comme c'est le cas
figure II.7.1), en présence d'un terme de courant de surface g. On obtient la condition aux limites
|
(II.7.11) |
 |
Nous modélisons la présence d'un obstacle opaque (figure II.7.1) dans le domaine  par la condition sur la trace tangentielle du champ
électrique sur le bord intérieur
par la condition sur la trace tangentielle du champ
électrique sur le bord intérieur
 ,
,
|
(II.7.12) |
 |
appelée condition de conducteur parfait ou condition sur un objet métallique. Notons aussi la condition aux limites retenue pour les équations intégrales qui modélise
la présence d'une couche de matériau de faible épaisseur et de fort indice n (II.7.8) sur un objet métallique,
|
(II.7.13) |
 |
où
 , (
, ( ), est l'impédance de la couche ou l'impédance intrinsèque définie par (II.7.9). Cette condition est appelée condition de
Léontovich ou condition d'impédance. En pratique, le terme ``fort indice'' signifie que l'on doit avoir
), est l'impédance de la couche ou l'impédance intrinsèque définie par (II.7.9). Cette condition est appelée condition de
Léontovich ou condition d'impédance. En pratique, le terme ``fort indice'' signifie que l'on doit avoir  [59].
[59].
Figure II.7.1:
Problème type en domaine borné.
|
|
Toutes ces conditions aux limites peuvent se résumer, en introduisant un opérateur de bord noté  (qui pourra être une simple fonction du bord
(qui pourra être une simple fonction du bord  à valeur complexe,
ou être constant), de norme strictement inférieure à 1, et à l'aide d'une fonction g terme source d'énergie finie au bord du domaine, par
à valeur complexe,
ou être constant), de norme strictement inférieure à 1, et à l'aide d'une fonction g terme source d'énergie finie au bord du domaine, par
|
(II.7.14) |
 |
où les coefficients
 et
et  sont réels et permettent d'adimensionner les quantités à sommer.
Nous retrouvons la condition aux limites de conducteur parfait (II.7.12) pour
sont réels et permettent d'adimensionner les quantités à sommer.
Nous retrouvons la condition aux limites de conducteur parfait (II.7.12) pour
 , la condition aux limites absorbante pour
, la condition aux limites absorbante pour
 dans le vide (II.7.11) ou même sur une frontière dans un milieu non absorbant où
dans le vide (II.7.11) ou même sur une frontière dans un milieu non absorbant où
 et de même pour
et de même pour  , la condition d'impédance intrinsèque (II.7.13) pour
, la condition d'impédance intrinsèque (II.7.13) pour
 dans un matériau non absorbant, une relation
d'impédance quelconque pour
dans un matériau non absorbant, une relation
d'impédance quelconque pour
(la transformée de Cayley de Q) dans un matériau absorbant.
Résoudre le problème de Maxwell harmonique en domaine borné signifie donc trouver le couple
(<I>E,<I>H) vérifiant à la fois II.7.5 dans
 et II.7.14 sur
et II.7.14 sur
 . Notons que dans le vide, les lois II.7.5 deviennent, puisque
. Notons que dans le vide, les lois II.7.5 deviennent, puisque
 et
et  ,
,
|
(II.7.15) |
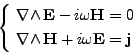 |
pour un terme source <I>j de divergence nulle dans  (et
<I>m=0, ce qui est une hypothèse physique), et
(et
<I>m=0, ce qui est une hypothèse physique), et
|
(II.7.16) |
 |
Nous constatons que la relation de Maxwell-Faraday implique la relation de Gauss magnétique. Il en est de même de la relation de Gauss électrique en l'absence de courant et de charges
extérieures. Nous reformulons donc le problème de Maxwell dans l'espace des fonctions de divergence nulle dans le vide (
 ) par
) par
|
(II.7.17) |
 |
où les termes sources <I>m et <I>j sont aussi de divergence nulle. En présence de matériau, nous considérerons le cas décrit par la figure
type II.7.1 où les coefficients  et
et  sont constants par morceaux
sont constants par morceaux
|
(II.7.18) |
 |
La situation de la figure II.7.1 nous permet de rester dans les espaces de fonctions de divergence nulle par morceaux avec les relations de saut
(II.7.19), ou relations de continuité des traces tangentielles des champs, aux interfaces de discontinuité des perméabilité
et permittivité entre les deux domaines  et
et  . Nous supposons que l'interface de discontinuité est assez régulière pour y définir une normale
. Nous supposons que l'interface de discontinuité est assez régulière pour y définir une normale  .
.
|
(II.7.19) |
 |





suivant: II.7.1.2 Cadre mathématique usuel et résultats d'existence
monter: II.7.1 Rappels sur le problème de Maxwell.
précédent: II.7.1 Rappels sur le problème de Maxwell.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() décrit par la permittivité
décrit par la permittivité ![]() et la perméabilité
et la perméabilité ![]() , fonctions de
la fréquence f (ou de la pulsation
, fonctions de
la fréquence f (ou de la pulsation
![]() ) et de la position notée <I>X. Les ondes électromagnétiques décrites par les champs électrique
<I>E et magnétique <I>H sont éventuellement perturbées par des termes sources volumiques d'énergie finie, la densité de courant électrique <I>j et
la densité de charge magnétique <I>m. Nous formulons en outre les hypothèses suivantes:
) et de la position notée <I>X. Les ondes électromagnétiques décrites par les champs électrique
<I>E et magnétique <I>H sont éventuellement perturbées par des termes sources volumiques d'énergie finie, la densité de courant électrique <I>j et
la densité de charge magnétique <I>m. Nous formulons en outre les hypothèses suivantes:
![]() et la perméabilité
et la perméabilité ![]() définissent la célérité ou vitesse de propagation c des ondes électromagnétiques par
définissent la célérité ou vitesse de propagation c des ondes électromagnétiques par
![]() dans le domaine
dans le domaine ![]()

![]() à l'infini (dans un domaine complémentaire d'un borné) dans le vide où
à l'infini (dans un domaine complémentaire d'un borné) dans le vide où
![]() (d'après II.7.4):
(d'après II.7.4):
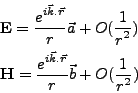


![]() sur son bord extérieur
sur son bord extérieur
![]() (que l'on suppose placé dans le vide, comme c'est le cas
figure II.7.1), en présence d'un terme de courant de surface g. On obtient la condition aux limites
(que l'on suppose placé dans le vide, comme c'est le cas
figure II.7.1), en présence d'un terme de courant de surface g. On obtient la condition aux limites
![]() (qui pourra être une simple fonction du bord
(qui pourra être une simple fonction du bord ![]() à valeur complexe,
ou être constant), de norme strictement inférieure à 1, et à l'aide d'une fonction g terme source d'énergie finie au bord du domaine, par
à valeur complexe,
ou être constant), de norme strictement inférieure à 1, et à l'aide d'une fonction g terme source d'énergie finie au bord du domaine, par
![]() et II.7.14 sur
et II.7.14 sur
![]() . Notons que dans le vide, les lois II.7.5 deviennent, puisque
. Notons que dans le vide, les lois II.7.5 deviennent, puisque
![]() et
et ![]() ,
,