I.3.3 Etude théorique de l'ordre de convergence.

Le but de cette section est d'expliquer sur le plan théorique les résultats observés numériquement dans la section précédente. La raison pour laquelle l'ordre de convergence du problème homogène est majoré par une loi linéaire du nombre de fonctions de base par élément est enracinée dans l'utilisation de fonctions de base solutions du problème dual homogène. Une technique de dualité, équivalente au lemme d'Aubin-Nitsche, étend cette loi aux problèmes non homogènes.

Pour simplifier l'étude, nous allons nous intéresser aux normes sur le bord $\Gamma$.

L'étude est découpée en plusieurs parties.

1. Nous établissons l'estimation qui relie l'erreur (x-x_h) à l'erreur d'interpolation ||(I-P_h)x|| (section I.3.3.1, lemme 8):
   
   $$\vert\vert(I-A)(x-x_h)\vert\vert \leq 2 \vert\vert(I-P_h)x\vert\vert \ ,$$
   
   
   où P_h dénote le projecteur orthogonal sur l'espace de discrétisation V_h.
2. Par une technique de dualité, nous montrons (section I.3.3.2, théorème 6) une estimation en normes de Sobolev à exposants négatifs (supposant une régularité plus faible que L²) sur $\Gamma$: pour tout s>1/2,
   
   $$\vert\vert x-x_h\vert\vert _{H^{-s}(\Gamma)} \leq 2 \vert\v... ...ert}{\displaystyle \vert\vert\psi\vert\vert _{H^{s}(\Gamma)}}}$$
   
   
   où $y(\psi)$ est donné par la solution du problème de Helmholtz homogène.
3. Avec l'hypothèse 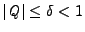$\vert{{\mathit Q}}\vert \leq \delta < 1$, on obtient des majorations de l'erreur à la frontière (lemme 9) en norme $L^2(\Omega)$
   
   $$\vert\vert x-x_h\vert\vert _{L^2(\Gamma)} \leq \frac{\displa... ...splaystyle \sqrt{1-\delta^2}} \vert\vert(I-P_h)x\vert\vert \ .$$
   
   

4. Nous estimons l'erreur u-u_h au bord à partir de l'erreur x-x_h (lemme 10, section I.3.3.3.2) dans tout espace de Sobolev pour s positif ou nul
   
   $$\vert\vert u-u_h\vert\vert _{H^{-s}(\Gamma)} \leq \frac{\dis... ...style 2\omega}\vert\vert x-x_h\vert\vert _{H^{-s}(\Gamma)} \ .$$
   
   

5. Dans le cas particulier du problème de Helmholtz homogène (f=0 dans (I.0.1)) et u de classe C^[(p+1)]/2, nous estimons le terme d'interpolation ||(I-P_h)x||_V (section I.3.3.4, théorème 7). Pour p fonctions de base par élément construites à partir d'ondes planes, et pour un maillage régulier, on a
   
   $$\vert\vert(I-P_h)x\vert\vert _V \leq C h^{[(p-1)]/2-1/2} \vert\vert u\vert\vert _{C^{[(p+1)]/2}(\Omega)} \ .$$
   
   

6. A l'aide du théorème 7 nous obtenons les résultats finaux concernant les estimations d'ordres de convergence en des normes sur la frontière (section I.3.3.5). Dans le cas spécifiquement homogène, nous avons des estimations en norme $L^2 ( \Gamma)$ (corollaire 4, lemme 9). Une estimation plus générale (sans hypothèse sur f) complète ce résultat (corollaire 5). Cette estimation est valable dans un espace de Sobolev à exposant négatif et est meilleure que celle dans l'espace $L^2 ( \Gamma)$ (de fonctions plus régulières). Le lemme 10 stipule que les estimations sont du même ordre sur u-u_h que sur x-x_h.

Cette étude ne concerne que des normes sur le bord. Nous ne faisons pas d'estimation intérieure. De telles estimations peuvent faire l'objet d'une étude ultérieure par une technique de dualité appropriée.