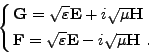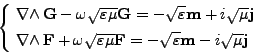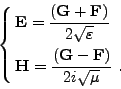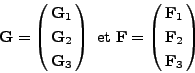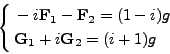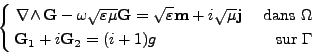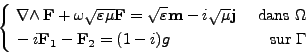suivant: II.7.2 La formulation ultra-faible et ses propriétés.
monter: II.7.1 Rappels sur le problème de Maxwell.
précédent: II.7.1.2 Cadre mathématique usuel et résultats d'existence
Table des matières
Index
II.7.1.3 Découplage des équations de Maxwell.
On considère les équations de Maxwell sur le couple
(<I>E,<I>H) dans  ,
,
|
(II.7.34) |
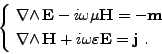 |
Posons
|
(II.7.35) |
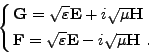 |
Un calcul élémentaire montre que le problème (II.7.47) est équivalent à
|
(II.7.36) |
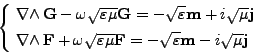 |
avec
|
(II.7.37) |
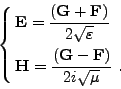 |
Autrement dit, les champs <I>G et <I>F sont solutions d'équations différentielles découplées.
Dans un matériau réel, la condition aux limites absorbante est
|
(II.7.38) |
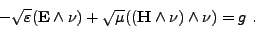 |
Substituons le couple
(<I>G,<I>F) au couple
(<I>E,<I>H). On obtient, sur  ,
,
|
(II.7.39) |
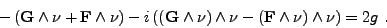 |
On écrit les composantes de <I>G et <I>F dans un repère orthonormé direct dont le troisième axe est  ,
,
|
(II.7.40) |
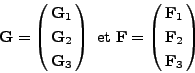 |
La relation (II.7.52) devient
|
(II.7.41) |
 |
En multipliant la deuxième équation par i et en sommant avec la première, puis en multipliant la première par i et en sommant avec la deuxième, on a les équations découplées
|
(II.7.42) |
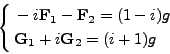 |
Pour résumer, nous avons à résoudre les systèmes découplés
|
(II.7.43) |
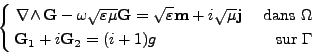 |
et
|
(II.7.44) |
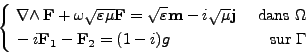 |





suivant: II.7.2 La formulation ultra-faible et ses propriétés.
monter: II.7.1 Rappels sur le problème de Maxwell.
précédent: II.7.1.2 Cadre mathématique usuel et résultats d'existence
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() ,
,