suivant: III.B.2 Reconstruction des champs électrique et magnétique.
monter: III.B.1 Construction du système linéaire.
précédent: III.B.1.3.3 Une propriété supplémentaire des matrices.
Table des matières
Index
Nous calculons les 2pK termes du second membre b (II.8.2) dans des cas particuliers où les termes sources du problème de Maxwell permettent un calcul analytique.
Pour une résolution des équations de Maxwell avec des termes sources plus compliqués, il faudrait assembler les termes du second membre de la formulation discrète grâce à une intégration
numérique.
Nous utiliserons les notations de la section (III.B.1.1) en définissant des termes d'indice 0 par
|
(III.B.48) |
 |
et de même pour hk,j,l,0n (III.B.4), Zk,j,l,0n (III.B.5) et fk,jl,0 (III.B.6).
On suppose que  est une fonction constante pour une face frontière donnée
est une fonction constante pour une face frontière donnée  .
Pour
.
Pour  , on a d'après (II.8.9),
, on a d'après (II.8.9),
et
ou
|
(III.B.49) |
 |
et
|
(III.B.50) |
 |
Nous allons expliciter (III.B.49) et (III.B.50) dans les cas suivants.
- i)
- Calculons le second membre b pour une condition aux limites donnée par un terme de bord g tel que
où le couple
(<I>E,<I>H) est donné par
On pose
|
(III.B.51) |
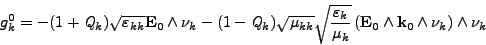 |
Alors,
|
(III.B.52) |
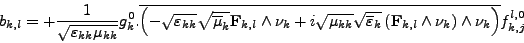 |
et
|
(III.B.53) |
 |
Notons que la complexité de ce calcul est équivalente à celle du calcul des termes matriciels (section III.B.1.3).
- ii)
- Pour
 , nous avons:
, nous avons:
|
(III.B.54) |
 |
et
|
(III.B.55) |
 |
puisque
 .
.
- iii)
- Calculons le second membre b pour des termes sources
(<I>m,<I>j) donnés par
|
(III.B.56) |
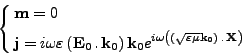 |
où
 sont tels que
|<I>E0|=|<I>k0|=1 et
sont tels que
|<I>E0|=|<I>k0|=1 et
 .
Notons que le champ
(<I>E,<I>H) donné par
.
Notons que le champ
(<I>E,<I>H) donné par
|
(III.B.57) |
 |
est solution des équations de Maxwell dans  . Notons en outre que
(<I>E,<I>H) ne fait pas partie de l'espace des fonctions de base puisque
. Notons en outre que
(<I>E,<I>H) ne fait pas partie de l'espace des fonctions de base puisque
 .
.
La contribution volumique de ce terme source
(<I>m,<I>j) non nul est
|
(III.B.58) |
 |
Il reste à calculer l'intégrale 3D,
donnée annexe III.D.1.3 en posant
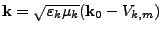 .
.





suivant: III.B.2 Reconstruction des champs électrique et magnétique.
monter: III.B.1 Construction du système linéaire.
précédent: III.B.1.3.3 Une propriété supplémentaire des matrices.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() est une fonction constante pour une face frontière donnée
est une fonction constante pour une face frontière donnée ![]() .
Pour
.
Pour ![]() , on a d'après (II.8.9),
, on a d'après (II.8.9),