




suivant: I.3.4.2 Evolution numérique du conditionnement.
monter: I.3.4 Conditionnement de la matrice de produit
précédent: I.3.4 Conditionnement de la matrice de produit
Table des matières
Index
Dans l'annexe III.E.1, on montrera que pour p=3 fonctions de base par élément, on peut majorer le conditionnement de Dk
indépendamment de h. On montrera également que l'équirépartition des ondes planes maximise le déterminant de Dk indépendamment de la
géométrie de  . Nous montrons dans l'annexe III.E.2 que ce résultat se généralise au problème scalaire
de Helmholtz dans l'espace
. Nous montrons dans l'annexe III.E.2 que ce résultat se généralise au problème scalaire
de Helmholtz dans l'espace
 .
.
Dans le cas 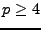 , nous avons de plus l'estimation suivante.
, nous avons de plus l'estimation suivante.
![\begin{proof}
% latex2html id marker 8868Soient $\lambda_{min}$\ la plus petit...
...displaymath}
q(p) \ge 2[p/2]-2 \ .
\end{displaymath}\end{description}\end{proof}](img341.gif)
Corollaire 6
Sous les mêmes hypothèses et les mêmes notations que celles des théorèmes 8 et 7,
l'ordre du conditionnement de la matrice hermitienne D du système linéaire est minoré par la fonction
2[p/2]-2
lorsque h tend vers zéro et pour p fonctions de base par élément, 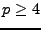 .
.





suivant: I.3.4.2 Evolution numérique du conditionnement.
monter: I.3.4 Conditionnement de la matrice de produit
précédent: I.3.4 Conditionnement de la matrice de produit
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() . Nous montrons dans l'annexe III.E.2 que ce résultat se généralise au problème scalaire
de Helmholtz dans l'espace
. Nous montrons dans l'annexe III.E.2 que ce résultat se généralise au problème scalaire
de Helmholtz dans l'espace
![]() .
.
![]() , nous avons de plus l'estimation suivante.
, nous avons de plus l'estimation suivante.
![]()