




suivant: III.B.1.3 Assemblage des matrices.
monter: III.B.1 Construction du système linéaire.
précédent: III.B.1.1 Introduction, notations.
Table des matières
Index
III.B.1.2 Forme des matrices.
La construction de Galerkin de l'espace de discrétisation implique que la matrice D-C du système linéaire est essentiellement creuse. Nous avons montré,
section II.8.2.3, la nullité, dans le vide, de certains des termes des matrices. Nous illustrons ces résultats par l'exemple de la configuration de
la figure (III.B.1) qui est un maillage d'une pyramide à base quadrangulaire  en 4 éléments tétraédriques. La figure est une projection
du maillage sur le plan de base de la pyramide. Dans cette figure, 2 éléments sont dans le vide où
en 4 éléments tétraédriques. La figure est une projection
du maillage sur le plan de base de la pyramide. Dans cette figure, 2 éléments sont dans le vide où
 . L'existence d'éléments dans le vide entraîne la nullité
de certains termes des matrices (lemme 19 p.
. L'existence d'éléments dans le vide entraîne la nullité
de certains termes des matrices (lemme 19 p. ![[*]](crossref.gif) ). C'est pourquoi nous avons repéré les différents types d'interfaces
). C'est pourquoi nous avons repéré les différents types d'interfaces  selon les cas suivants.
selon les cas suivants.
- i)
- Cas général où
 est une face entre deux éléments
est une face entre deux éléments  et
et  ,
,  possédant du matériau,
possédant du matériau,  quelconque.
quelconque.
- ii)
- Cas simplifié où les deux éléments sont placés dans le vide.
- iii)
- Cas d'une interface (
 ) telle que
) telle que  soit dans le vide et
soit dans le vide et  possède un matériau.
possède un matériau.
En plus de la réduction de la taille mémoire (remarque 40 p. ![[*]](crossref.gif) ), ces différents cas ont une importance pour l'optimisation du calcul numérique (par exemple
en utilisant les propriétés de la section III.B.1.3.3).
), ces différents cas ont une importance pour l'optimisation du calcul numérique (par exemple
en utilisant les propriétés de la section III.B.1.3.3).
Figure III.B.1:
Exemple de configuration des éléments.
![\begin{figure}\begin{center}
\begin{tabular}[htbp]{c}\setlength{\unitlength}{0...
...{0pt}[0pt][0pt]{\large ii)}}}
\end{picture}\end{tabular}\end{center}\end{figure}](img1193.gif) |
La matrice D est nulle partout sauf sur des blocs diagonaux de taille 2p x 2p. Nous notons
D<I>F,<I>F les termes d'indices
 correspondant aux produits scalaires des
fonctions de type <I>F,
D<I>F,<I>G pour les indices
correspondant aux produits scalaires des
fonctions de type <I>F,
D<I>F,<I>G pour les indices 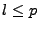 et
et 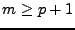 et
D<I>G,<I>G pour
et
D<I>G,<I>G pour
 . La forme de la matrice hermitienne D est la suivante:
. La forme de la matrice hermitienne D est la suivante:
où la notation
D3,2<I>F,<I>G (resp.
D4,1<I>F,<I>G) est la contribution de la face 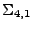 entre
entre 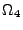 et
et 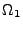 (resp. de la face
(resp. de la face 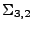 entre
entre 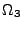 et
et
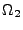 ) au calcul de
D3<I>F,<I>G (resp.
D4<I>F,<I>G). On remarque que
D3<I>F,<I>G=D3,2<I>F,<I>G (resp.
D4<I>F,<I>G=D4,1<I>F,<I>G) puisque les
contributions des autres faces sont nulles.
) au calcul de
D3<I>F,<I>G (resp.
D4<I>F,<I>G). On remarque que
D3<I>F,<I>G=D3,2<I>F,<I>G (resp.
D4<I>F,<I>G=D4,1<I>F,<I>G) puisque les
contributions des autres faces sont nulles.
De même, la matrice C est de la forme essentiellement creuse suivante
On remarque que certains sous-blocs de couplage de fonctions de types différents (couplage des fonctions de type <I>F avec des fonctions de type <I>G ou l'inverse) sont nuls. C'est le cas des sous-blocs
C3,4 et C4,3, couplages sur une interface dans le vide puisque ces deux éléments sont dans le vide. On remarque que certains sous-blocs de C sont nuls pour des termes de couplage de fonctions de même type (types <I>F ou <I>G). C'est le cas des blocs C3,3 et C4,4, couplages sur des faces de bord dans le vide (puisque ces deux éléments sont dans le vide).





suivant: III.B.1.3 Assemblage des matrices.
monter: III.B.1 Construction du système linéaire.
précédent: III.B.1.1 Introduction, notations.
Table des matières
Index
Cessenat Olivier
2007-04-21
![[*]](crossref.gif) ). C'est pourquoi nous avons repéré les différents types d'interfaces
). C'est pourquoi nous avons repéré les différents types d'interfaces ![]() en 4 éléments tétraédriques. La figure est une projection
du maillage sur le plan de base de la pyramide. Dans cette figure, 2 éléments sont dans le vide où
en 4 éléments tétraédriques. La figure est une projection
du maillage sur le plan de base de la pyramide. Dans cette figure, 2 éléments sont dans le vide où
![]() . L'existence d'éléments dans le vide entraîne la nullité
de certains termes des matrices (lemme 19 p.
. L'existence d'éléments dans le vide entraîne la nullité
de certains termes des matrices (lemme 19 p. ![[*]](crossref.gif) ). C'est pourquoi nous avons repéré les différents types d'interfaces
). C'est pourquoi nous avons repéré les différents types d'interfaces ![]() selon les cas suivants.
selon les cas suivants.
![[*]](crossref.gif) ), ces différents cas ont une importance pour l'optimisation du calcul numérique (par exemple
en utilisant les propriétés de la section III.B.1.3.3).
), ces différents cas ont une importance pour l'optimisation du calcul numérique (par exemple
en utilisant les propriétés de la section III.B.1.3.3).
![]() correspondant aux produits scalaires des
fonctions de type <I>F,
D<I>F,<I>G pour les indices
correspondant aux produits scalaires des
fonctions de type <I>F,
D<I>F,<I>G pour les indices ![]() et
et ![]() et
D<I>G,<I>G pour
et
D<I>G,<I>G pour
![]() . La forme de la matrice hermitienne D est la suivante:
. La forme de la matrice hermitienne D est la suivante:
![\begin{displaymath}
D = \left[ \begin{array}{cccc}
\begin{array}{cc}
D_1^{{{\mat...
...hbf G}},{{\mathbf G}}} \\
\end{array} \\
\end{array} \right]
\end{displaymath}](img1197.gif)
![\begin{displaymath}
C = \left[ \begin{array}{cccc}
\begin{array}{cc}
C_{1,1}^{{{...
...G}},{{\mathbf F}}} & 0 \\
\end{array} \\
\end{array} \right]
\end{displaymath}](img1204.gif)