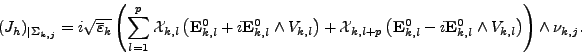suivant: II.10.1.2 Propagation libre en milieu homogène.
monter: II.10.1 Tests de validation du code.
précédent: II.10.1 Tests de validation du code.
Table des matières
Index
II.10.1.1 Présentation des tests.
Les simulations effectuées ont essentiellement porté sur trois types de géométries figurées en II.10.1.
- Le domaine représenté par la figure II.10.1 a) est un cube centré sur l'origine de longueur L.
- Le domaine représenté par la figure II.10.1 b) est un cube centré sur l'origine et d'arête de longueur a placé dans un autre cube plus gros
d'arête de longueur b. Le domaine de calcul dans le cas b) est donc le volume compris entre les deux cubes. Nous avons utilisé les cas a=30 centimètres et b=50 centimètres
puis a=50 centimètres et b=70 centimètres. Notons que dans les deux cas la frontière artificielle est très proche de l'objet.
- Afin de réaliser des simulations qui sont susceptibles d'être proches de problèmes industriels, nous avons considéré le cas du cône dans un cylindre décrit dans la note
technique de Christophe Le Potier
[42]. Le cône parfaitement conducteur (impénétrable aux ondes électromagnétiques) d'axe de symétrie de révolution z mesure 1,3 m et le point le plus haut pour z
positif est à 0,6 m. La base du cône est un disque de rayon 0,18 m. La frontière bornant le domaine est un cylindre de 2,3 m de hauteur et de rayon 0,4 m, le point le plus
élevé du cylindre pour z positif est à 1,4 m. Le cône est éventuellement revêtu de deux couches de matériau. Ces couches sont de 5 centimètres d'épaisseur, l'une
est à la pointe du cône pour z>0, l'autre est au culot pour
 II.101.
II.101.
Figure II.10.1:
Exemples de domaines  utilisés.
utilisés.
![\includegraphics[width=0.29\textwidth]{cub1.ps}](img1001.gif) |
![\includegraphics[width=0.29\textwidth]{cub2.ps}](img1002.gif) |
![\includegraphics[height=0.33\textwidth]{cone.ps}](img1003.gif) |
| a) Propagation libre, |
b) Diffraction sur un cube, |
c) Coupe du cône revêtu. |
|
Nous utiliserons dans cette section les notions de ``scattering'', calcul en ``champ total'' ou en ``champ diffracté'', de conditions de conducteur parfait ou d'absorbant parfait.
Ces notions ont déjà été vues pour l'étude du problème de Helmholtz, nous les clarifions pour le problème de Maxwell.
Définition 18 (``scattering'' et propagation libre)
Dans toutes les simulations effectuées, nous considérons le problème de ``scattering'' ou propagation d'une onde plane (que nous appelons onde plane incidente) dans un milieu
sans source d'énergie. Le mot ``scattering'' signifie diffraction lorsque l'onde plane incidente rencontre un objet impénétrable aux ondes électromagnétiques. Lorsque le
milieu de propagation a des permittivités et perméabilités variables, le terme ``scattering'' signifie diffusion: nous n'employons pas ce terme ambigü que l'on risque de confondre avec d'autres phénomènes physiques. En l'absence de diffraction et de diffusion, nous parlerons
de propagation libre dans un milieu homogène.
Définition 19 (champ total)
On appelle ``calcul en champ total'' le problème de Maxwell dans un milieu sans source d'énergie volumique dont la condition aux limites est vérifiée par une onde plane sur
la frontière extérieure
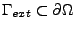 (évidemment non vide). La condition aux limites sur la frontière intérieure
(évidemment non vide). La condition aux limites sur la frontière intérieure  de l'objet diffractant
(éventuellement vide) est vérifiée par la solution nulle. Le problème se met sous la forme
de l'objet diffractant
(éventuellement vide) est vérifiée par la solution nulle. Le problème se met sous la forme
|
(II.10.1) |
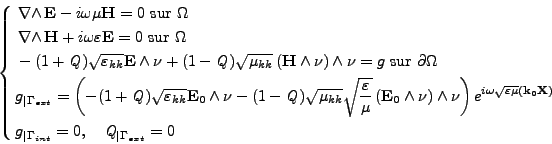 |
où l'on a
|
(II.10.2) |
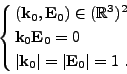 |
Notons que lorsque
 et
et  et
et  les permittivité et perméabilité sont constantes dans tout le domaine
les permittivité et perméabilité sont constantes dans tout le domaine  , le couple
(<I>E,<I>H) donné par
, le couple
(<I>E,<I>H) donné par
|
(II.10.3) |
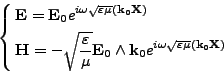 |
est solution du problème II.10.1. C'est ce que nous avons appelé le problème de propagation libre dans un milieu homogène
(définition 18). Noter que la solution (II.10.3) est analytique et s'intègre facilement sur des surfaces planes.
Définition 20 (champ diffracté)
On note
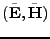 la solution du problème (II.10.1). Soit
où
(<I>E0
la solution du problème (II.10.1). Soit
où
(<I>E0,
<I>H
0) est le champ incident. On dit que
(
<I>E,
<I>H) est le champ diffracté. Dans le cas où les caractéristiques du domaine

sont celles du
vide partout
(
<I>E,
<I>H) est la solution du système
|
(II.10.4) |
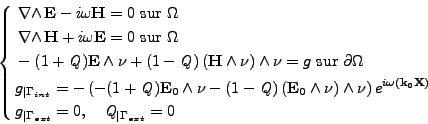 |
avec
(<I>k0,
<I>E
0) vérifiant les conditions (
II.10.2). Cela correspond à supposer que l'onde plane incidente est issue de la frontière
intérieure

(
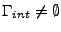
).
Définition 21 (condition d'absorbant parfait)
La condition d'absorbant parfait correspond à prendre
 sur la frontière de l'objet
sur la frontière de l'objet  dans la condition aux limites (II.7.11), ou de façon équivalente par la condition (II.7.13) pour une impédance Z égale à 1. On a alors
dans la condition aux limites (II.7.11), ou de façon équivalente par la condition (II.7.13) pour une impédance Z égale à 1. On a alors
|
(II.10.5) |
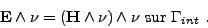 |
Définition 22 (condition de conducteur parfait)
La condition de conducteur parfait correspond à prendre
 sur la frontière de l'objet
sur la frontière de l'objet  dans la condition aux limites (II.7.11). On obtient
dans la condition aux limites (II.7.11). On obtient
|
(II.10.6) |
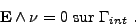 |
La direction incidente
<I>k0 du problème de ``scattering'' est définie dans un repère sphérique par des angles 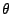 et
et 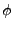 qui seront par la suite toujours indiqués dans
la convention
qui seront par la suite toujours indiqués dans
la convention
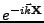 en degrés. Les conventions de polarisation, modes TM ou TE, sont aussi indiquées dans la convention
en degrés. Les conventions de polarisation, modes TM ou TE, sont aussi indiquées dans la convention
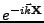 . Toutes ces conventions sont clairement expliquées dans [7] par J.L. Bonnefoy.
En revanche, les vecteurs directions de propagation et polarisations sont donnés dans la convention utilisée dans le code
. Toutes ces conventions sont clairement expliquées dans [7] par J.L. Bonnefoy.
En revanche, les vecteurs directions de propagation et polarisations sont donnés dans la convention utilisée dans le code
 soit
soit
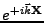 .
.
Dans tout ce chapitre on utilise deux types d'approximations des champs, types « G » et « H ».
Définition 23 (Approximation «
G » des courants totaux)
C'est l'approximation naturelle des traces tangentielles utilisant la quantité approchée
 des deux côtés d'une interface. Cette approximation est issue des calculs (III.B.62) et (III.B.64) des traces tangentielles de
<I>Hh
des deux côtés d'une interface. Cette approximation est issue des calculs (III.B.62) et (III.B.64) des traces tangentielles de
<I>Hh section
III.B.2.2 p.
![[*]](crossref.gif)
. Le courant total
Jh,
pour un calcul en champ total, est donné par les formules ci-dessous:
- sur une face de bord
 ,
,
- sur une face intérieure
-
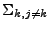 ,
,
Définition 24 (Approximation «
H » des courants totaux)
C'est l'approximation valable seulement pour des matériaux à caractéristiques électromagnétiques réelles et un problème de Maxwell homogène. Cette approximation est issue
de la formule (III.B.60) des traces tangentielles de
<I>Hh section
III.B.2.1 p.
![[*]](crossref.gif)
. Le courant total
Jh, pour un calcul en champ total,
est donné par la formule





suivant: II.10.1.2 Propagation libre en milieu homogène.
monter: II.10.1 Tests de validation du code.
précédent: II.10.1 Tests de validation du code.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() et
et ![]() et
et ![]() les permittivité et perméabilité sont constantes dans tout le domaine
les permittivité et perméabilité sont constantes dans tout le domaine ![]() , le couple
(<I>E,<I>H) donné par
, le couple
(<I>E,<I>H) donné par
![]() et
et ![]() qui seront par la suite toujours indiqués dans
la convention
qui seront par la suite toujours indiqués dans
la convention
![]() en degrés. Les conventions de polarisation, modes TM ou TE, sont aussi indiquées dans la convention
en degrés. Les conventions de polarisation, modes TM ou TE, sont aussi indiquées dans la convention
![]() . Toutes ces conventions sont clairement expliquées dans [7] par J.L. Bonnefoy.
En revanche, les vecteurs directions de propagation et polarisations sont donnés dans la convention utilisée dans le code
. Toutes ces conventions sont clairement expliquées dans [7] par J.L. Bonnefoy.
En revanche, les vecteurs directions de propagation et polarisations sont donnés dans la convention utilisée dans le code
![]() soit
soit
![]() .
.
![[*]](crossref.gif) . Le courant total Jh,
pour un calcul en champ total, est donné par les formules ci-dessous:
. Le courant total Jh,
pour un calcul en champ total, est donné par les formules ci-dessous:
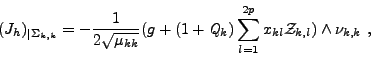

![[*]](crossref.gif) . Le courant total Jh, pour un calcul en champ total,
est donné par la formule
. Le courant total Jh, pour un calcul en champ total,
est donné par la formule