suivant: II.9.1.1.3 Etude du cas général, construction d'un
monter: II.9.1.1 Etude du noyau de la matrice
précédent: II.9.1.1.1 Etude du noyau de M pour
Table des matières
Index
Dans le cas général, pour tout N, on déduit de
 les
les
 relations
relations
|
(II.9.26) |
 |
et de
 les
les
 relations
relations
|
(II.9.27) |
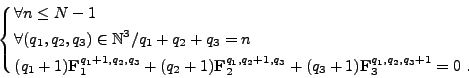 |
Remarquons que pour  et
et  , les premières relations du rotationnel s'écrivent aussi
, les premières relations du rotationnel s'écrivent aussi
qui, en faisant la somme des trois équations ci-dessus pour tout
 , impliquent naturellement les
, impliquent naturellement les
 relations
relations
|
(II.9.28) |
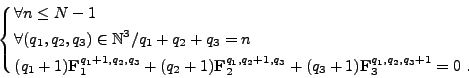 |
Cessenat Olivier
2007-04-21
![]() les
les
 relations
relations

 relations
relations
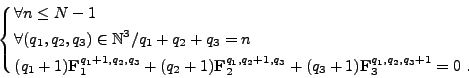

 relations
relations