




suivant: II.9.1.3 Bilan de l'étude de l'erreur d'interpolation.
monter: II.9.1.2 Etude de l'image de la matrice
précédent: II.9.1.2.3 Conclusion, pas de généralisation de la
Table des matières
Index
Dans le cas général, la matrice PM étudiée est
|
(II.9.43) |
 |
de taille
En exprimant
<I>Eil et Vli en fonctions de  et
et 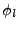 (d'après les relations II.9.35), on a le système défini
(d'après les relations II.9.35), on a le système défini
- pour
q1+q2+q3 = N-1, par
|
(II.9.44) |
 |
- et pour q2+q3 = N, par
|
(II.9.45) |
 |
Nous allons démontrer l'existence de p=(N+1)(N+3) couples
 tels que la matrice PM, dont les lignes sont données par (II.9.44) et (II.9.45), soit inversible.
tels que la matrice PM, dont les lignes sont données par (II.9.44) et (II.9.45), soit inversible.
Pour cela, il suffit de montrer les deux conjectures suivantes.
- Le déterminant d'une matrice dont le terme générique est fi(xj) où les fonctions fi sont linéairement indépendantes n'est pas nul partout. Si les fonctions fi sont continues
et libres sur tout intervalle, l'ensemble des
 annulant le déterminant est de mesure nulle. Ceci fait l'objet du lemme 22.
annulant le déterminant est de mesure nulle. Ceci fait l'objet du lemme 22.
- Les fonctions construisant la matrice sont linéairement indépendantes sur
 dans tout sous domaine de mesure non nulle de
dans tout sous domaine de mesure non nulle de
![$[0\ldots \pi]\times[-\pi\ldots \pi]$](img949.gif) .
Ceci fait l'objet du lemme 23.
.
Ceci fait l'objet du lemme 23.

Nous avons montré l'indépendance linéaire des fonctions de
 que sont les fonctions (II.9.44) et
(II.9.45) dans les cas particuliers N=1 et N=2. Le but était d'en ``intuiter'' un raisonnement général.
Ces preuves sont extrêmement calculatoires et consistent à développer les expressions en
que sont les fonctions (II.9.44) et
(II.9.45) dans les cas particuliers N=1 et N=2. Le but était d'en ``intuiter'' un raisonnement général.
Ces preuves sont extrêmement calculatoires et consistent à développer les expressions en  en fonction de
en fonction de  puis par des multiplications par des matrices inversibles
à faire apparaître que les fonctions utilisées sont des combinaisons linéaires de fonctions libres utilisées une seule fois dans tous les termes. Ces preuves sont longues à faire:
pour N=1 on obtient 8 fonctions, pour N=2 on obtient 15 fonctions. Nous ne donnons pas ces preuves: trop explicites, elles n'ont pas fait se dégager un raisonnement valable pour tout N.
puis par des multiplications par des matrices inversibles
à faire apparaître que les fonctions utilisées sont des combinaisons linéaires de fonctions libres utilisées une seule fois dans tous les termes. Ces preuves sont longues à faire:
pour N=1 on obtient 8 fonctions, pour N=2 on obtient 15 fonctions. Nous ne donnons pas ces preuves: trop explicites, elles n'ont pas fait se dégager un raisonnement valable pour tout N.
Après une longue recherche, essayant des raisonnements par récurrence ou par l'absurde ou recherchant les points communs avec Helmholtz bi ou tridimensionnel, nous avons réussi à montrer le lemme 23 par les trois étapes que sont les sous-lemmes 24, 25 et 26.
Remarque 43 Remarquons qu'il est essentiel de ne pas rajouter la famille
g3(
q1,
q2,
q3) pour

. En effet, on déduit de
que
|
(II.9.49) |
 |
Lemme 24
La famille décrite par (II.9.47) et (II.9.48) est une sous famille de la famille décrite par (II.9.47) pour N+1. L'espace vectoriel engendré
par la famille (II.9.47) est le même que celui engendré par la famille
|
(II.9.50) |
 |
avec

Lemme 25
La famille f1 décrite par (II.9.50) est libre. Il en est de même de la famille f2 (et de la famille g2).
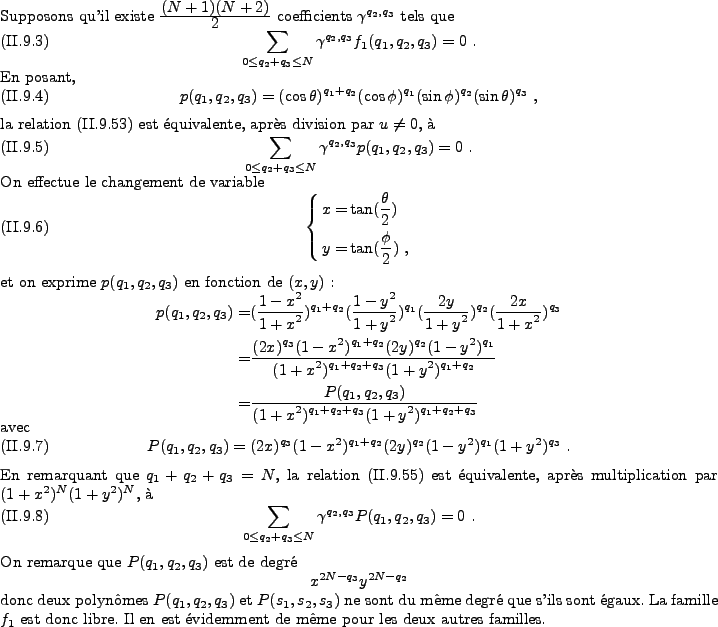
![\begin{proof}
% latex2html id marker 30087
{\bf [du lemme \ref{conjecture.m3dord...
...eft( [f_2] \times <f_1>_{(q_1,q_2,q_3)} \right) \ .
\end{displaymath}\end{proof}](img971.gif)
Lemme 26
Aucune fonction
f1(r1,r2,r3) pour r1+r2+r3=N n'est dans l'espace vectoriel [f2].







suivant: II.9.1.3 Bilan de l'étude de l'erreur d'interpolation.
monter: II.9.1.2 Etude de l'image de la matrice
précédent: II.9.1.2.3 Conclusion, pas de généralisation de la
Table des matières
Index
Cessenat Olivier
2007-04-21



![]() que sont les fonctions (II.9.44) et
(II.9.45) dans les cas particuliers N=1 et N=2. Le but était d'en ``intuiter'' un raisonnement général.
Ces preuves sont extrêmement calculatoires et consistent à développer les expressions en
que sont les fonctions (II.9.44) et
(II.9.45) dans les cas particuliers N=1 et N=2. Le but était d'en ``intuiter'' un raisonnement général.
Ces preuves sont extrêmement calculatoires et consistent à développer les expressions en ![]() en fonction de
en fonction de ![]() puis par des multiplications par des matrices inversibles
à faire apparaître que les fonctions utilisées sont des combinaisons linéaires de fonctions libres utilisées une seule fois dans tous les termes. Ces preuves sont longues à faire:
pour N=1 on obtient 8 fonctions, pour N=2 on obtient 15 fonctions. Nous ne donnons pas ces preuves: trop explicites, elles n'ont pas fait se dégager un raisonnement valable pour tout N.
puis par des multiplications par des matrices inversibles
à faire apparaître que les fonctions utilisées sont des combinaisons linéaires de fonctions libres utilisées une seule fois dans tous les termes. Ces preuves sont longues à faire:
pour N=1 on obtient 8 fonctions, pour N=2 on obtient 15 fonctions. Nous ne donnons pas ces preuves: trop explicites, elles n'ont pas fait se dégager un raisonnement valable pour tout N.
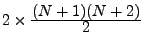 fonctions données par
fonctions données par
![\begin{proof}
% latex2html id marker 30087
{\bf [du lemme \ref{conjecture.m3dord...
...eft( [f_2] \times <f_1>_{(q_1,q_2,q_3)} \right) \ .
\end{displaymath}\end{proof}](img971.gif)

