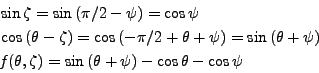suivant: II.9.1.2.2 Un contre-exemple inattendu dans le cas
monter: II.9.1.2 Etude de l'image de la matrice
précédent: II.9.1.2 Etude de l'image de la matrice
Table des matières
Index
Nous cherchons à caractériser le rang de la matrice M dans le cas N=0 et à établir la condition sur le choix des fonctions de base pour que le
système (II.9.20) admette une solution.
Pour N=0 et pour p=3 fonctions
<I>Fl la matrice M est la matrice carrée des polarisations:
Mm,l = <I>Fl,m, soit d'après
(II.9.36) la matrice
Mm,l = <I>Elm. Dans une base orthonormée directe bien choisie (cf annexe (III.E.3)),
cette matrice est de la forme
|
(II.9.39) |
![\begin{displaymath}
M = \left[ \begin{array}{lll}
\sin{(\theta)}\cos{(\phi)} +i\...
...- \cos{(\theta)} & -i\sin{(\zeta)} & 0 \\
\end{array} \right]
\end{displaymath}](img903.gif) |
où les angles
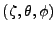 définissent les trois vecteurs polarisations
<I>E1,<I>E2,<I>E3:
définissent les trois vecteurs polarisations
<I>E1,<I>E2,<I>E3:
|
(II.9.40) |
![\begin{displaymath}%
\left[ \begin{array}{l}
\cos{(\theta)}\cos{(\phi)} \\
\cos...
...\begin{array}{l}
0 \\
0 \\
1 \\
\end{array} \right] \ .
\end{displaymath}](img905.gif) |
Le déterminant de (II.9.39) est nul si et seulement si
|
(II.9.41) |
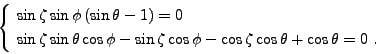 |
Nous allons montrer que M est inversible si et seulement les trois directions de propagation
V1,V2,V3 (II.9.35) sont distinctes
deux à deux.
Pour cela, étudions la contraposée, c'est-à-dire les conditions pour que les relations (II.9.41) soient vérifiées simultanément.
- Si
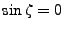 alors si
alors si 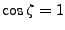 les vecteurs 2 et 3 de directions de propagation sont égaux. Si
les vecteurs 2 et 3 de directions de propagation sont égaux. Si
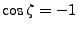 alors
alors
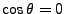 qui implique que les
vecteurs 1 et 2 ou 3 sont égaux.
qui implique que les
vecteurs 1 et 2 ou 3 sont égaux.
- Si
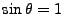 alors
alors
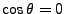 et les vecteurs 1 et 3 de directions de propagation sont égaux.
et les vecteurs 1 et 3 de directions de propagation sont égaux.
- Si
 alors si
alors si 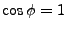 , on a
, on a
et si 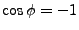 ,
,
La fonction
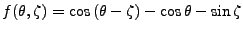 est une fonction de signe constant.
On pose
est une fonction de signe constant.
On pose
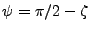 , alors
, alors
En posant
 et
et
 , on a
, on a
Le cas q=1 signifie
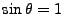 qui est exclu dans la situation précédente. De même pour t=1. Le cas qt=1 signifie
qui est exclu dans la situation précédente. De même pour t=1. Le cas qt=1 signifie
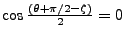 soit
soit
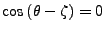 et puisque
et puisque
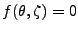 on a
on a
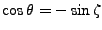 et
et
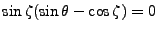 . Le cas
. Le cas 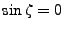 est déjà traité, le cas
est déjà traité, le cas
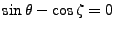 impliquerait que les
vecteurs 1 et 2 soient égaux.
impliquerait que les
vecteurs 1 et 2 soient égaux.
Le résumé de l'étude de l'image de M pour N=0 est donné dans la
Proposition 15
Dans le cas N=0, la matrice M constituée de
lignes et de
p=3
colonnes est inversible si et seulement si les trois directions de propagations des ondes planes choisies sont distinctes deux à deux.





suivant: II.9.1.2.2 Un contre-exemple inattendu dans le cas
monter: II.9.1.2 Etude de l'image de la matrice
précédent: II.9.1.2 Etude de l'image de la matrice
Table des matières
Index
Cessenat Olivier
2007-04-21
![\begin{displaymath}
M = \left[ \begin{array}{lll}
\sin{(\theta)}\cos{(\phi)} +i\...
...- \cos{(\theta)} & -i\sin{(\zeta)} & 0 \\
\end{array} \right]
\end{displaymath}](img903.gif)
![\begin{displaymath}%
\left[ \begin{array}{l}
\cos{(\theta)}\cos{(\phi)} \\
\cos...
...\begin{array}{l}
0 \\
0 \\
1 \\
\end{array} \right] \ .
\end{displaymath}](img905.gif)