




suivant: II.9.1.2 Etude de l'image de la matrice
monter: II.9.1.1 Etude du noyau de la matrice
précédent: II.9.1.1.2 Relations de Gauss obtenues à partir
Table des matières
Index
Nous allons montrer l'indépendance des
 relations
relations
|
(II.9.29) |
 |
et des
 relations
relations
|
(II.9.30) |
 |
Remarquons que si l'on ordonne le vecteur
<I>Fiq1,q2,q3 par blocs croissants en fonction de q1+q2+q3, puis en sous-blocs croissants en fonction de i, puis encore
en sous-sous-blocs décroissants en fonction de q1, nous pourrons faire apparaître les relations (II.9.29)
et (II.9.30) sous une forme triangulaire supérieure comme dans le cas N=1 à l'aide d'une matrice P.
Notons qu'une fonction Q vérifiant ce rangement n'est pas unique, puisqu'on a toute liberté d'ordonner les derniers blocs en fonction de q2 ou en fonction de q3.
Nous avons choisi de ranger ces derniers blocs de façon décroissante en fonction de q2 (c'est-à-dire de façon croissante avec q3 puisque le bloc à ranger
est donné pour q1 et q1+q2+q3 fixé).
La donnée de la fonction Q nous permet d'expliciter entièrement la matrice M, dont le terme Mm,l (où m est l'indice de ligne et l de colonne) est donné
par (II.9.21) avec
m=Q(i,q1,q2,q3). On vérifie que la fonction Q définie ci-dessous dans la Définition
17 correspond bien à un tel rangement.
Définition 17 (Fonction bijective
Q)
- Le premier terme est Q(1,0,0,0)=1.
- Pour tout
 tel que
tel que  , on a la relation de récurrence
, on a la relation de récurrence
Q(1,n,0,0)=Q(1,n-1,0,0)+3*Cn+12
croissante en fonction de n.
- Pour tout
 tel que
tel que 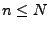 , et pour
, et pour  , on a la relation de récurrence
, on a la relation de récurrence
Q(i,n,0,0)=Q(i-1,n,0,0)+Cn+12
croissante en fonction de i.
- Pour tout
 tel que
tel que 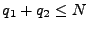 ,
,  et
et  , et pour
, et pour  , on a la relation de récurrence
, on a la relation de récurrence
Q(i,q1-1,q2+1,0)=Q(i,q1,q2,0)+(q2+1)
décroissante en fonction de q1.
- Pour tout
 tel que
tel que
 ,
,  et
et  , et pour
, et pour  , on a la relation de récurrence
, on a la relation de récurrence
Q(i,q1,q2-1,q3+1)=Q(i,q1,q2,q3)+1
décroissante en fonction de q2, croissante en fonction de q3.
Remarque 40 On déduit de la définition de
Q les relations de récurrence supplémentaires ci-dessous.
- Pour tout
 tel que
tel que
 ,
,  , et pour
, et pour  , on a la relation de récurrence
, on a la relation de récurrence
Q(i,q1,q2,q3)=Q(i-1,q1,q2,q3)+Cn+12
croissante en fonction de i.
- Pour tout
 tel que
tel que
 ,
,  et
et  , et pour
, et pour  , on a la relation de récurrence
, on a la relation de récurrence
Q(i,q1-1,q2+1,q3)=Q(i,q1,q2,q3)+(q2+q3+1)
décroissante en fonction de q1.
Remarque 41 On déduit de la définition de
Q les relations d'ordre ci-dessous.
On définit alors la matrice P comme dans le cas N=1.
- La matrice P est non nulle sur la diagonale. La diagonale est ordonnée en quatre blocs croissants. Le bloc a) est constitué de
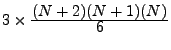 termes qui correspondent aux équations du rotationnel. Le bloc b) est constitué de
termes qui correspondent aux équations du rotationnel. Le bloc b) est constitué de
 termes qui correspondent aux équations de divergence.
Les blocs c) et d) sont constitués des (N+1)(N+3) termes manquant pour compléter la matrice P de façon à ce qu'aucun terme de la diagonale ne soit nul.
Le bloc c) est constitué de
termes qui correspondent aux équations de divergence.
Les blocs c) et d) sont constitués des (N+1)(N+3) termes manquant pour compléter la matrice P de façon à ce qu'aucun terme de la diagonale ne soit nul.
Le bloc c) est constitué de
 termes et le bloc d) de
termes et le bloc d) de
 termes.
Nous présentons la diagonale de P sous deux formes,
termes.
Nous présentons la diagonale de P sous deux formes,
et, pour
k=Q(i,q1,q2,q3), toujours sous la forme croissante (d'après la remarque 42),
On vérifie que les termes des blocs ci-dessus sont bien ordonnés de façon croissante d'après la remarque 42.
En particulier, les termes du bloc c) sont rangés avant les termes du bloc d) d'après la relation (II.9.33).
- La matrice P est non nulle sur une partie supérieure correspondant aux équations du rotationnel. On note
ce qui nous permet de prendre, comme représentants de la classe d'équivalence définie par ``modulo 3'', non pas {0,1,2} mais {1,2,3}.
Alors, pour  et pour tout
et pour tout
 tel que
tel que
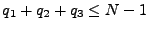 , on a
, on a
et
où l'on vérifie que  puisque les termes sont rangés en fonction croissante de q1+q2+q3 (cf (II.9.31)).
puisque les termes sont rangés en fonction croissante de q1+q2+q3 (cf (II.9.31)).
- La matrice P est non nulle sur une partie supérieure correspondant aux équations de divergence. Pour tout
 et pour tout
et pour tout
 tel
que
q1+q2+q3 = N-1, on a
tel
que
q1+q2+q3 = N-1, on a
où l'on vérifie que  . En effet, pour q1+q2+q3 fixé, on range les termes en fonction de i, et on a ici j>i (cf (II.9.32)).
. En effet, pour q1+q2+q3 fixé, on range les termes en fonction de i, et on a ici j>i (cf (II.9.32)).
- Les autres termes de la matrice P sont tous nuls.
La matrice P est triangulaire supérieure de diagonale non nulle: son déterminant est égal à
et est donc non nul si et seulement si  .
P est donc inversible.
.
P est donc inversible.
Le produit
P[<I>F] est le vecteur dont les
premières lignes sont nulles.
Il en est de même de la matrice dont la l-ième
colonne est
[<I>Fl] puisque les fonctions de base vérifient les relations sur le rotationnel
et la divergence.
On a donc
De façon équivalente, puisque la matrice PM a
lignes non nulles et p colonnes, on a le lemme suivant.
Lemme 21
Le rang de la matrice M, noté rang(M), vérifie





suivant: II.9.1.2 Etude de l'image de la matrice
monter: II.9.1.1 Etude du noyau de la matrice
précédent: II.9.1.1.2 Relations de Gauss obtenues à partir
Table des matières
Index
Cessenat Olivier
2007-04-21
 relations
relations
 relations
relations
 relations
relations
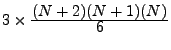 termes qui correspondent aux équations du rotationnel. Le bloc b) est constitué de
termes qui correspondent aux équations du rotationnel. Le bloc b) est constitué de
 termes qui correspondent aux équations de divergence.
Les blocs c) et d) sont constitués des (N+1)(N+3) termes manquant pour compléter la matrice P de façon à ce qu'aucun terme de la diagonale ne soit nul.
Le bloc c) est constitué de
termes qui correspondent aux équations de divergence.
Les blocs c) et d) sont constitués des (N+1)(N+3) termes manquant pour compléter la matrice P de façon à ce qu'aucun terme de la diagonale ne soit nul.
Le bloc c) est constitué de
 termes et le bloc d) de
termes et le bloc d) de
 termes.
Nous présentons la diagonale de P sous deux formes,
termes.
Nous présentons la diagonale de P sous deux formes,




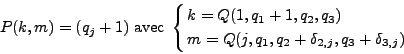


![\begin{displaymath}\left\{ \null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\stru...
...r
& rang(M) \le \min{[(N+1)(N+3),p]} \ . \cr
\crcr}}\, \right. \end{displaymath}](img896.gif)