Nous présentons des formules de calcul des traces des champs sur les arêtes du maillage, formules qui présentent l'avantage d'être facilement calculables informatiquement et qui sont une alternative au calcul précédent (formules (III.B.67) et (III.B.68)) qui utilisait l'opérateur de divergence surfacique.
En effet, on peut approcher les traces de <I>E et <I>H sur une arête quelconque du maillage par une combinaison linéaire des traces tangentielles sur les faces contenant cette arête.
Supposons connues les traces tangentielles suivantes sur les faces
![]() et
et
![]() :
:

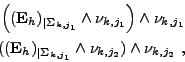
| (III.B.72) |
| (III.B.73) | 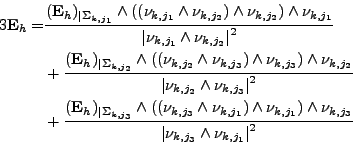 |