next up previous contents index
suivant: I.3.3.3.2 Estimation sur la frontière de u-uh. monter: I.3.3.3 Estimations d'énergie sur la frontière. précédent: I.3.3.3 Estimations d'énergie sur la frontière.   Table des matières   Index


I.3.3.3.1 Estimation sur la frontière de x-xh.

Nous étudions ici la norme du résidu 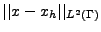$\vert\vert x-x_h\vert\vert _{L^2(\Gamma)}$ par rapport à l'erreur d'interpolation ||(I-Ph)x||. Ceci est l'équivalent du lemme de Céa.

Lemme 9   Soit ${{\mathit Q}}$ (l'opérateur de bord du problème de Helmholtz (I.0.1)) constant tel que $\vert{{\mathit Q}}\vert \leq \delta < 1$. Soit $x \in V$ la solution de (I.1.27) et $x_h \in V_h$ la solution de (I.2.1). Soit Ph le projecteur orthogonal sur l'espace Vh. Nous avons
(I.3.14) \begin{displaymath} \mbox{\fbox{$\vert\vert x-x_h\vert\vert _{L^2(\Gamma)} \leq ... ...yle \sqrt{1-\delta^2}} \vert\vert(I-P_h)x\vert\vert _V \ . $}} \end{displaymath}


\begin{proof} % latex2html id marker 7793Posons $\varepsilon_h = (x-x_h)$\ et ... ...rt\varepsilon_h\vert\vert _{\Gamma} \ . \crcr}}\, \end{equation}\par \end{proof}


Cessenat Olivier 2007-04-21