




suivant: I.1 Présentation de la Formulation ultra-faible.
monter: 1 Le problème de Helmholtz bidimensionnel.
précédent: 1 Le problème de Helmholtz bidimensionnel.
Table des matières
Index
Présentation de la première partie.
Cette première partie traite de l'application à un problème modèle de propagation d'ondes harmoniques, le problème de Helmholtz bidimensionnel
(ou, en abrégé, 2D). Ce travail reprend pour beaucoup la note CEA [15] et l'article accepté par SIAM Numerical Analysis [16].
Ce problème simplifié est étudié en détail car il permet de comprendre nombre de points difficiles de la problématique générale à
la fois de la formulation variationnelle et des équations d'ondes harmoniques. C'est pourquoi nous insisterons sur les difficultés inhérentes à
l'étude de tous les problèmes d'ondes harmoniques et sur les caractéristiques générales de la formulation.
Le problème de Helmholtz 2D découle de l'équation des ondes après avoir supprimé la dépendance en temps. Dans un domaine  borné de frontière
borné de frontière  assez régulière pour définir la normale presque partout, le problème harmonique se formalise, en normalisant la célérité de l'onde à 1 par
assez régulière pour définir la normale presque partout, le problème harmonique se formalise, en normalisant la célérité de l'onde à 1 par
|
(I.0.1) |
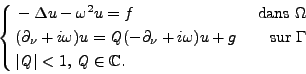 |
La dérivée normale extérieure est notée
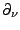 , la pulsation est notée
, la pulsation est notée  . Les conditions aux limites sont données par l'opérateur
. Les conditions aux limites sont données par l'opérateur  que l'on
supposera constant dans les preuves théoriques et de module strictement inférieur à l'unité. Néanmoins, dans les applications, notons qu'il est possible de poser
que l'on
supposera constant dans les preuves théoriques et de module strictement inférieur à l'unité. Néanmoins, dans les applications, notons qu'il est possible de poser
 (condition aux limites de Dirichlet) sur une partie de la frontière. De même, il est possible de poser
(condition aux limites de Dirichlet) sur une partie de la frontière. De même, il est possible de poser
 (condition aux limites de Neumann) sur une partie de la frontière.
L'essentiel est que le problème (I.0.1) soit bien posé et que la solution soit assez régulière (nous préciserons ultérieurement).
(condition aux limites de Neumann) sur une partie de la frontière.
L'essentiel est que le problème (I.0.1) soit bien posé et que la solution soit assez régulière (nous préciserons ultérieurement).
Notons qu'une condition aux limites absorbante est donnée par
 : c'est le condition aux limites d'ordre le plus bas. Cette condition est connue pour ne pas être très performante,
mais nous ne discuterons pas ce point qui ne fait pas l'objet de notre exposé.
: c'est le condition aux limites d'ordre le plus bas. Cette condition est connue pour ne pas être très performante,
mais nous ne discuterons pas ce point qui ne fait pas l'objet de notre exposé.
Rappelons que les difficultés principales de la résolution des problèmes d'ondes harmoniques résident dans la nature non coercive du problème et dans le fait que la solution
est oscillante, gouvernée par la longueur d'onde  liée à la pulsation
liée à la pulsation  par
par
Les méthodes classiques de l'analyse numérique utilisées pour résoudre les problèmes d'ondes harmoniques présentent l'inconvénient d'être basées sur la
décomposition en un système de la forme
|
(I.0.2) |
htmlcommentmark>
(F-K)u = b
|
où K est une perturbation compacte de l'opérateur coercif F (cf section I.1.1.2). L'injectivité de la matrice du système linéaire du
problème discret est conditionnée par le pas de discrétisation (proposition 5).
Par exemple, dans la méthode des Eléments Finis (en abrégé: ``FEM''), pour un problème bidimensionnel, un pas de discrétisation h vérifiant
|
(I.0.3) |
 |
est demandé sur le plan pratique pour assurer la stabilité du problème. La méthode par équations intégrales est aussi conditionnée par une telle relation, avec un
maillage surfacique de l'objet en  .
.
Au contraire des méthodes classiques, la stabilité de la nouvelle formulation n'est en aucun cas conditionnée par une relation entre la longueur d'onde et le pas de discrétisation.
De plus, nous verrons que l'ordre de convergence de la méthode est une fonction linéaire du nombre de fonctions de base par élément. Ceci n'est pas le cas dans
la méthode des éléments finis où l'ordre de convergence est en racine carrée du nombre de degrés de liberté du problème [17].
Ceci signifie que pour le même taux de précision la méthode issue de la formulation variationnelle ultra-faible (en abrégé: ``UWVF'') nécessite un stockage
informatique plus faible que la FEM.
L'idée de base de la formulation variationnelle ultra-faible est de considérer une nouvelle inconnue ainsi qu'un nouveau problème continu à partir desquels
on pourra remonter au problème initial et à sa solution (I.0.1). Pour cela, il convient de réaliser une partition de  ,
c'est-à-dire
,
c'est-à-dire
|
(I.0.4) |
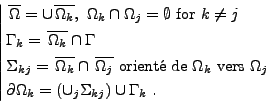 |
En pratique la partition est un maillage du domaine  . Les ensembles
. Les ensembles  sont les éléments. Nous noterons
sont les éléments. Nous noterons  les arêtes des interfaces et
les arêtes des interfaces et  les arêtes libres (figure 1).
les arêtes libres (figure 1).
Figure 1:
Partition d'un domaine  en éléments
en éléments 
![\begin{figure}\begin{center}
\begin{tabular}[htbp]{c}\setlength{\unitlength}{0...
...shortstack{\Huge\bf$\Omega$}}
\end{picture}\end{tabular}\end{center}\end{figure}](img31.gif) |
Nous définissons l'espace fonctionnel V de la formulation UWVF comme étant
|
(I.0.5) |
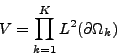 |
muni du produit scalaire naturel
|
(I.0.6) |
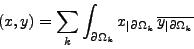 |
qui définit la norme ||.||V et la norme induite d'un opérateur  par:
par:
|
(I.0.7) |
 |
Remarque 1
Le cadre fonctionnel
V dépend du maillage, mais ce n'est pas un espace de discrétisation de dimension finie. Nous devrions nous y référer en notant l'indice
K du maillage.
Nous garderons néanmoins la notation
V, adoptée par [
25] et [
15] pour ne pas surcharger ce document.
Notons
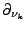 la dérivée normale extérieure
la dérivée normale extérieure
 . La valeur de l'inconnue notée x de la formulation UWVF est définie à partir de u la
solution de (I.0.1) comme étant:
. La valeur de l'inconnue notée x de la formulation UWVF est définie à partir de u la
solution de (I.0.1) comme étant:
|
(I.0.8) |
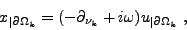 |
en faisant l'hypothèse de régularité
|
(I.0.9) |
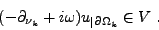 |
Cette hypothèse est valable dès que la solution u au problème (I.0.1) est suffisamment régulière.
Ainsi, la première caractéristique importante de la formulation UWVF est de mener à un problème dont les inconnues sont définies sur les interfaces. Le problème
résultant est un système linéaire de la forme
|
(I.0.10) |
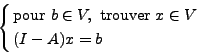 |
où A est un opérateur linéaire dans V vérifiant  et (I-A) inversible. Soulignons que cette formulation est générale à toute équation aux
dérivées partielles (EDP) linéaire elliptique (cf [27]).
et (I-A) inversible. Soulignons que cette formulation est générale à toute équation aux
dérivées partielles (EDP) linéaire elliptique (cf [27]).
La présentation de la formulation est organisée dans cette partie en cinq chapitres dont nous donnons ci-dessous les points essentiels.
- La section I.1 présente la nouvelle formulation. Sous l'hypothèse de régularité:
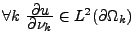 , nous définissons x et V
par (I.0.8) et (I.0.5).
Nous montrons (théorème 3) que, moyennant un opérateur de relèvement, la nouvelle formulation variationnelle
est équivalente au problème de Helmholtz (I.0.1). Ceci montre que la formulation UWVF est bien posée.
L'espace test de la formulation est constitué de fonctions z, dont les restrictions zk à
, nous définissons x et V
par (I.0.8) et (I.0.5).
Nous montrons (théorème 3) que, moyennant un opérateur de relèvement, la nouvelle formulation variationnelle
est équivalente au problème de Helmholtz (I.0.1). Ceci montre que la formulation UWVF est bien posée.
L'espace test de la formulation est constitué de fonctions z, dont les restrictions zk à
 sont construites à partir de fonctions e,
données par
sont construites à partir de fonctions e,
données par
|
(I.0.11) |
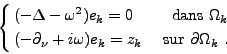 |
Ces équations sont les équations adjointes homogènes (i.e. f=0 dans  ) des équations du problème de Helmholtz (I.0.1).
On montre alors que la formulation a la propriété suivante.
) des équations du problème de Helmholtz (I.0.1).
On montre alors que la formulation a la propriété suivante.
Proposition 1
Il existe un opérateur A dans 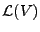 et b dans V tels que (I-A)x=b et
et b dans V tels que (I-A)x=b et
|
(I.0.12) |
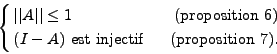 |
- La section I.2 présente le procédé de discrétisation par une méthode de Galerkin. La solution approchée xh
est cherchée dans un sous-espace Vh de V, Vh étant de dimension finie. Nous montrons comment définir et calculer une solution approchée uh de
u la solution du problème de départ (I.0.1) à partir de xh. L'espace de Galerkin Vh est construit à l'aide
de p fonctions de base zkl,l=1..p sur tout élément
 (avec k variant de 1 à K) qui sont des solutions du problème homogène
dual (I.0.11) et de support inclus dans
(avec k variant de 1 à K) qui sont des solutions du problème homogène
dual (I.0.11) et de support inclus dans  .
Le problème discret s'écrit formellement
.
Le problème discret s'écrit formellement
|
(I.0.13) |
(I-Ph A) xh = Ph b
|
et mène au système linéaire de dimension finie pK :
|
(I.0.14) |
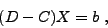 |
où
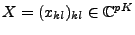 et
et
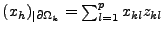 . Nous affirmons alors
. Nous affirmons alors
Proposition 2
Le système (I.0.14) est inversible pour tout paramètre de discrétisation h (théorème 5).
La matrice (D-C) du système linéaire est creuse.
L'utilisation d'ondes planes pour la construction des fonctions de base permet un calcul par une formule analytique des coefficients des matrices D et C.
De par le fait que  , on montre qu'il existe un algorithme itératif convergent pour résoudre le système linéaire discret.
Remarquons que l'on commande la qualité de l'approximation à l'aide de deux paramètres: le paramètre de taille du maillage (qui définit
l'espace de la formulation continue V) et le nombre de fonctions de base.
, on montre qu'il existe un algorithme itératif convergent pour résoudre le système linéaire discret.
Remarquons que l'on commande la qualité de l'approximation à l'aide de deux paramètres: le paramètre de taille du maillage (qui définit
l'espace de la formulation continue V) et le nombre de fonctions de base.
- La section I.3 est dédiée à l'étude de l'ordre de convergence de la méthode. Cette section est
divisée en deux parties. Une partie numérique montre le comportement ``linéaire'' I.01 de l'ordre de convergence en fonction du nombre de fonctions
de base par élément. Une partie théorique mène aux deux résultats essentiels que sont les deux propositions suivantes.
A l'aide d'une technique de dualité on montre l'existence d'une loi de convergence linéaire dans le cas non homogène (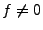 ) dans un espace de Sobolev
d'exposant négatif.
) dans un espace de Sobolev
d'exposant négatif.
- La section I.4.2 présente diverses simulations numériques: deux cas tests où l'on calculera les valeurs de u,
deux cas tests de scattering avec des calculs de Section Efficace Radar (SER).
- Nous présentons la formulation variationnelle sur un problème de Helmholtz à coefficients variables section I.5.





suivant: I.1 Présentation de la Formulation ultra-faible.
monter: 1 Le problème de Helmholtz bidimensionnel.
précédent: 1 Le problème de Helmholtz bidimensionnel.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() borné de frontière
borné de frontière ![]() assez régulière pour définir la normale presque partout, le problème harmonique se formalise, en normalisant la célérité de l'onde à 1 par
assez régulière pour définir la normale presque partout, le problème harmonique se formalise, en normalisant la célérité de l'onde à 1 par
![]() : c'est le condition aux limites d'ordre le plus bas. Cette condition est connue pour ne pas être très performante,
mais nous ne discuterons pas ce point qui ne fait pas l'objet de notre exposé.
: c'est le condition aux limites d'ordre le plus bas. Cette condition est connue pour ne pas être très performante,
mais nous ne discuterons pas ce point qui ne fait pas l'objet de notre exposé.
![]() liée à la pulsation
liée à la pulsation ![]() par
par
![]() ,
c'est-à-dire
,
c'est-à-dire
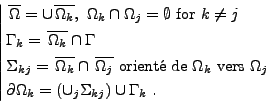
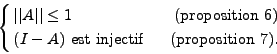
![]() , on montre qu'il existe un algorithme itératif convergent pour résoudre le système linéaire discret.
Remarquons que l'on commande la qualité de l'approximation à l'aide de deux paramètres: le paramètre de taille du maillage (qui définit
l'espace de la formulation continue V) et le nombre de fonctions de base.
, on montre qu'il existe un algorithme itératif convergent pour résoudre le système linéaire discret.
Remarquons que l'on commande la qualité de l'approximation à l'aide de deux paramètres: le paramètre de taille du maillage (qui définit
l'espace de la formulation continue V) et le nombre de fonctions de base.