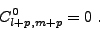On a alors, pour
soit, par définition de fk,jl,m (III.B.6),
| (III.B.29) |
pour
- Le bloc supérieur gauche des fonctions de type <I>F, termes C0l,m, se calcule par
(III.B.30) 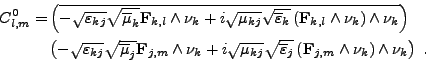
- Le bloc supérieur droit des couplages des fonctions de type <I>F avec les fonctions de type <I>G, termes C0l,m+p, se calcule par
et, lorsque(III.B.31) 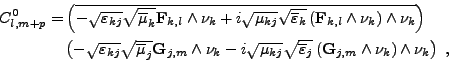
 sur
sur  et
et  , on a
, on a
(III.B.32) 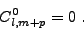
- Le bloc inférieur gauche des couplages des fonctions de type <I>G avec les fonctions de type <I>F, termes C0l+p,m, se calcule par
et, lorsque(III.B.33) 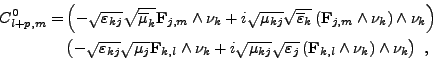
 sur
sur  et
et  , on a
, on a
(III.B.34) 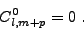
- Le bloc inférieur droit des fonctions de type <I>G, termes
C0l+p,m+p, se calcule par
D'après la remarque 49 on peut exprimer Cl+p,m+p en fonction de <I>Fk,l et <I>Fj,m:(III.B.35) 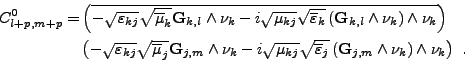
ce qui montre que, si(III.B.36) 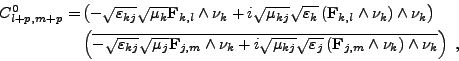
 et
et  sont réels sur
sont réels sur  et
et  , alors
, alors
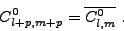
| (III.B.37) |
où l'on reconnaît le terme fk,kl,m (III.B.7), que nous savons calculer analytiquement par la formule (III.B.8). Il reste à calculer le bloc C0 donné par
pour
- Le bloc supérieur gauche des fonctions de type <I>F, termes C0l,m, se calcule par
et, lorsque(III.B.39) 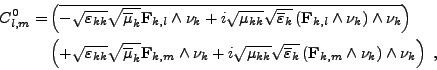
 sur
sur  , on a
, on a
(III.B.40) 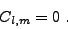
- Le bloc supérieur droit des couplages des fonctions de type <I>F avec les fonctions de type <I>G, termes C0l,m+p, se calcule par
D'après la remarque 49, on peut exprimer C0l,m+p en fonction de <I>Fk,l et <I>Fk,m. On a en effet(III.B.41) 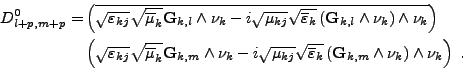
(III.B.42) 
- Le bloc inférieur gauche des couplages des fonctions de type <I>G avec les fonctions de type <I>F, termes C0l+p,m, se calcule par
ce qui montre que, si(III.B.43) 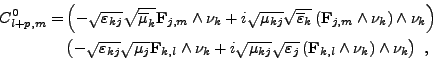
 et
et  sont réels sur
sont réels sur  , alors
, alors
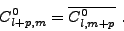
- Le bloc inférieur droit des fonctions de type <I>G, termes
C0l+p,m+p, se calcule par
D'après la remarque 49, on peut exprimer C0l+p,m+p en fonction de <I>Fk,l et <I>Fk,m:(III.B.44) 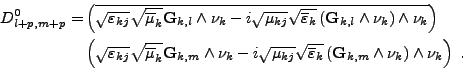
et, lorsque(III.B.45) 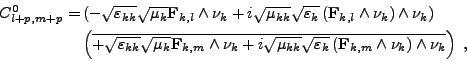
 sur
sur  , on a
, on a