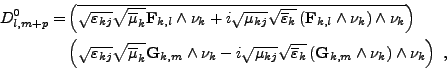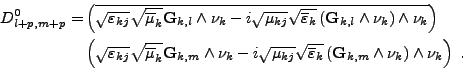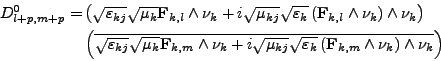suivant: III.B.1.3.2 Calcul de la matrice C.
monter: III.B.1.3 Assemblage des matrices.
précédent: III.B.1.3 Assemblage des matrices.
Table des matières
Index
III.B.1.3.1 Calcul de la matrice D.
Nous notons Dk,jl,m la contribution de la face  pour le calcul de Dkl,m dans (II.8.6). On a alors, pour
pour le calcul de Dkl,m dans (II.8.6). On a alors, pour
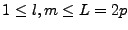 , à l'aide des
notations (III.B.3) et (III.B.12),
, à l'aide des
notations (III.B.3) et (III.B.12),
|
(III.B.18) |
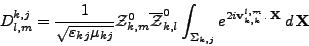 |
soit, par définition de fk,kl,m (III.B.7),
|
(III.B.19) |
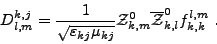 |
Nous savons calculer analytiquement le terme fk,kl,m par la formule (III.B.8). Il reste à calculer la matrice hermitienne D0 donnée par
|
(III.B.20) |
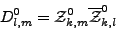 |
pour
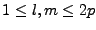 .
Cette matrice est constituée de quatre blocs selon les valeurs des indices par rapport à p. Dans les formules énumérées ci-dessous, les indices l et m sont tels que
.
Cette matrice est constituée de quatre blocs selon les valeurs des indices par rapport à p. Dans les formules énumérées ci-dessous, les indices l et m sont tels que
 .
.
- Le bloc supérieur gauche des fonctions de type <I>F, termes D0l,m, se calcule par
|
(III.B.21) |
 |
- Le bloc supérieur droit des produits scalaires de types
(<I>F,<I>G), termes D0l,m+p, se calcule par
|
(III.B.22) |
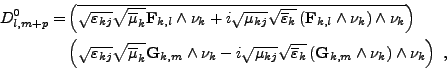 |
ou, d'après la remarque 49, par
|
(III.B.23) |
 |
Si
 sur
sur  et
et  alors
alors
|
(III.B.24) |
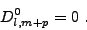 |
- Le bloc inférieur droit des fonctions de type <I>G, termes
D0l+p,m+p, se calcule par
|
(III.B.25) |
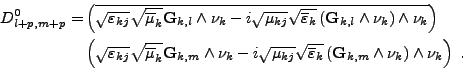 |
D'après la remarque 49, on peut exprimer Dl+p,m+p en fonction de
<I>Fk,l et
<I>Fk,m:
|
(III.B.26) |
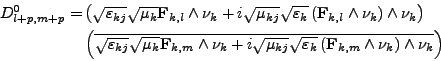 |
ce qui montre que si  et
et  sont réels sur
sont réels sur  alors
alors





suivant: III.B.1.3.2 Calcul de la matrice C.
monter: III.B.1.3 Assemblage des matrices.
précédent: III.B.1.3 Assemblage des matrices.
Table des matières
Index
Cessenat Olivier
2007-04-21
![]() pour le calcul de Dkl,m dans (II.8.6). On a alors, pour
pour le calcul de Dkl,m dans (II.8.6). On a alors, pour
![]() , à l'aide des
notations (III.B.3) et (III.B.12),
, à l'aide des
notations (III.B.3) et (III.B.12),