| (III.E.17) | ![\begin{displaymath}%
\null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\strut\hfil...
...1}^{N}{\lambda_n [\overline{w_n} {w_n}^{\top}] } \cr
\crcr}}\,
\end{displaymath}](img1546.gif) |
| (III.E.18) |  |
| (III.E.19) |
| (III.E.17) | ![\begin{displaymath}%
\null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\strut\hfil...
...1}^{N}{\lambda_n [\overline{w_n} {w_n}^{\top}] } \cr
\crcr}}\,
\end{displaymath}](img1546.gif) |
| (III.E.18) |  |
| (III.E.19) |
| (III.E.20) | ![\begin{displaymath}%
\null\,\vcenter{\openup\jot \let\\ =\@
\ialign{\strut\hfil...
...lpha} \sum_{n=1}^{N}{\lambda_n [w_n {w_n}^{*}] } \cr
\crcr}}\,
\end{displaymath}](img1550.gif) |
| (III.E.21) |  |
Nous pouvons maintenant commencer la preuve du théorème 20.
| (III.E.23) |  |
On pose:
| (III.E.24) |  |
| (III.E.25) | ![\begin{displaymath}%
\null\,\vcenter{\openup1\jot \let\\ =\@
\ialign{\strut\hfi...
...3D_3+S_4D_4) \cr
& D_n = [\vec{w}_n\otimes\vec{w}_n]
\crcr}}\,
\end{displaymath}](img1555.gif) |
a) Simplification du déterminant de D.
![]()
b) Découplage du déterminant en la géométrie et les fonctions de base.
c) Optimisation du déterminant.
d) Récapitulatif et fin du calcul du déterminant.
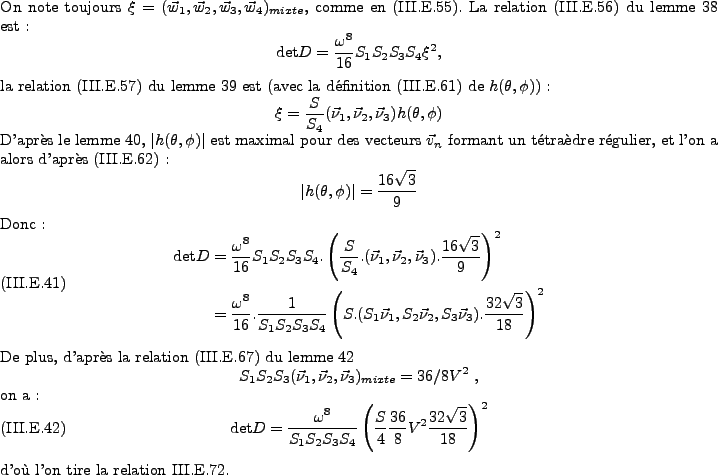
e) Majoration du conditionnement.
| (III.E.33) |
![\begin{displaymath}
\null\,\vcenter{\openup1\jot \let\\ =\@
\ialign{\strut\hfil...
...3D_3+S_4D_4) \cr
& D_n = [\vec{w}_n\otimes\vec{w}_n]
\crcr}}\,
\end{displaymath}](img1573.gif)
